|
|
|
![]()
![]() Geometric
construction of the pentagram, pentacle, pentagon, and the five
pointed star —
and spice it up here and there with three kinds of ten pointed stars
Geometric
construction of the pentagram, pentacle, pentagon, and the five
pointed star —
and spice it up here and there with three kinds of ten pointed stars
- sketch
a five pointed star on a clock template, for kids [yes, pick a
better shade of pink]. Tilt and rotate and double them
- draw
stars of pentagrams and pentagons
using a compass and straightedge (two geometric methods)
- construct
a pentacle directly inside your own circle
or with your
own sides length (point-to-point dimension). What you pick —
large or small —
will be a rational and therefore an exact measure
- tell
the diff between a pentacle and a pentagram and why there are
several pentacles
- determine
the inside and outside angles of a pentagram
- find
the golden proportions that are
inherent in a penta~ star and grow them, too
- make
a five-point star indirectly via pentagon tiling —
and vice versa
- create
fancy
five pointed stars plus a ten pointed hyperstar from a
half-square rectangle (in a new tab)
- double
a pentagon in one circle for a decagon
- get
the only harmonious ten pointed star of a decagram
by always skipping 6 points
- design
5 point stars as art forms —
inherit the energies if you stick to nature
- combine the up and down pointing pentacles into a brand new hyperstar. On five circles. You'll be in the micro but this is huge
- encircled
once or twice —
a star is on a single circle or in-between of two concentric circles
- built
from interlocking rings
- taken
as a shape of a human body
- upside down. Devil's in details
How to
What does it mean if a pentagram is
Symmetry in a five pointed star — there are several kinds of symmetry and .. ..
![]()
![]() A
perfect three
pointed
star can be had on a circle or semicircle —
and it's doubled for a regular six-point star or a hexagon already.
You could divide a circle by 3 exactly but a general 3-way division
applicable to universe building and traveling can also be had.
Hexagon and hexagram stars are behind viruses.
A
perfect three
pointed
star can be had on a circle or semicircle —
and it's doubled for a regular six-point star or a hexagon already.
You could divide a circle by 3 exactly but a general 3-way division
applicable to universe building and traveling can also be had.
Hexagon and hexagram stars are behind viruses.
![]() A
perfect square is a four pointed star
A
perfect square is a four pointed star
![]()
![]() An
eight pointed star and a twelve pointed
star share the same construction. Both stars
are perfect and both take you beyond counting as well
An
eight pointed star and a twelve pointed
star share the same construction. Both stars
are perfect and both take you beyond counting as well
![]()
![]()
16 and 24 pointed stars also share the same construction. Just as the eight and 12 pointed stars, they are in the 3:2 musical ratio and because the growth of stars in this ratio is unbounded we have a separate page on that (in a new tab)
How many perfect stars can you make with geometry? With arithmetic? Number 36 is (abundantly) divisible by 2, 3, 4, 6, 9, 12, and 18 – yet, you cannot make a perfect 36 pointed star
-
Geometry vs. Arithmetic is a very old topic, very unresolved, and very relevant; and
- Numbers are not just symbols. In a circle they make 1) stars on paper and 2) atoms in space
![]() A
comment on a seven pointed star
(heptagon). Hit a snag in a circle, but ..
A
comment on a seven pointed star
(heptagon). Hit a snag in a circle, but ..
Pentagon Pyramid. Fusion of numbers in three dimensions is good but it is not about averaging
The four sided Great Pyramid construction is via the golden proportion and has its own page (in a new tab)
|
A
five pointed star just for kids. If you can tell time you can sketch
this and other stars by hand. Oh, use the free template below at first. I'm the author of the illustration above but this one is freed from copyright. (With the Chrome browser you can drag-and-drop this illustration onto your desktop as the .gif file.) Have a look at some pics from the stone circle at Avebury in Wiltshire, UK. Draw a star, any perfect star. Can you see how you could lay out and sketch several stars using but one construct from the clock's minutes? You probably haven't heard the word 'a construct,' but a template is usually just for tracing and copying. Can you join the points by skipping some? Odd and even number of points makes a big difference. Here are the from-the-ground-up geometric constructions of eight and 16 point stars of a compass rose. [Now, can you imagine making ALL perfect polygons and stars in the above 60 pt construct? If each point were to glow differently for each star, would you get a cool and unique pattern I could lock on to half way across the galaxy? Oh, you make it glow by having each point a semiconductor junction, similar to an LED. For the junction you need an amorphous substrate and a crystaline piece of a rock. Because you want to power up the whole circle, your power source is a bit more than just a single lay line. Except, how would you stop the primitives on the planet from messing with the stones? Yeah, it is all sacred feminine kind of stuff. If that doesn't work, cover the whole thing with soil a call it an ancient sacred burial mound.] |

Intro
Historically,
geometric drawing of a pentagram star was considered a secret. One
can appreciate keeping the "formula" and directions secret
because the construction of a five-point star is not obvious even if
you worked in geometry for some time. Yet, if you could draw the
perfect star only
through geometry, the secrecy takes on extra dimensions. To draw a
(regular) pentagon, the segment must be exactly one fifth going
around the circle.
|
Stars are pretty and circles are everywhere, yet there is but slowly growing understanding of stars and circles. (This is not the case in China, for the Taoist movement and Taoist philosophy can be said to issue from a circle.) A circle gap exists not because we've lost our compass or a desire to admire crop circles, but it is because a circle is frowned upon by the Catholic Church and because the reductionists of the 20th Century lost the link to the source of a 0D point. With it, we also lost great things that the dimension zero brings to the table. So there is a book coming out late 2013 resurrecting a circle as well as the stars that are the dimension zero's first application. Oh, 99% of all moving energy in the universe is in spin and orbits. Not only that. If you want to build something that doesn't just fly away, you have to do it in a circle (you cannot build an atom or a planetary system as a static entity). Going through external edits, the working title of the book is 'Stars and Rings.' |
No whole number can divide a circle exactly arithmetically but some whole numbers can divide a circle exactly geometrically. This is the first differentiator between geometry and arithmetic. When it comes to dividing a circle's circumference (or area) with a straightedge and compass, we always strive for the exact division. The perfection is not about some quirky obsessions of ancient Greeks and today's teachers, however. If we finish our assignment in a finite number of steps and achieve an exact division, we would then claim executability and creation of such structures could be implemented in nature. Computer's arithmetic gives us precise — but not exact — answers when working with incommensurable (irrational and transcendental) numbers, but the geometric way can be exact and have much utility just because of that. We will apply the division of a circle in the atomic construction below. Yes, the exact construction is about the (exact) conservation of energy.
If the length of a circle's straight segment (cord) is exact, then the segment's length is unambiguous and can be expressed as a finite number. A finite number is also a rational number. If the cord's length were an irrational number then such number's sub-unity portion (mantissa) is infinite and we could not agree on its exact length — but we could agree on the exact distance between the two end points because the two end points can be constructed exactly geometrically. Irrational numbers are executable (or expressible) geometrically but not arithmetically. This is the second differentiator between geometry and arithmetic. You might skip on the diff between length and distance right now — later you may avail to the explanation and construction of the incommensurable numbers (irrationals and transcendentals).
Instructions on geometric division of a circle into five equal and exact parts — in five steps:
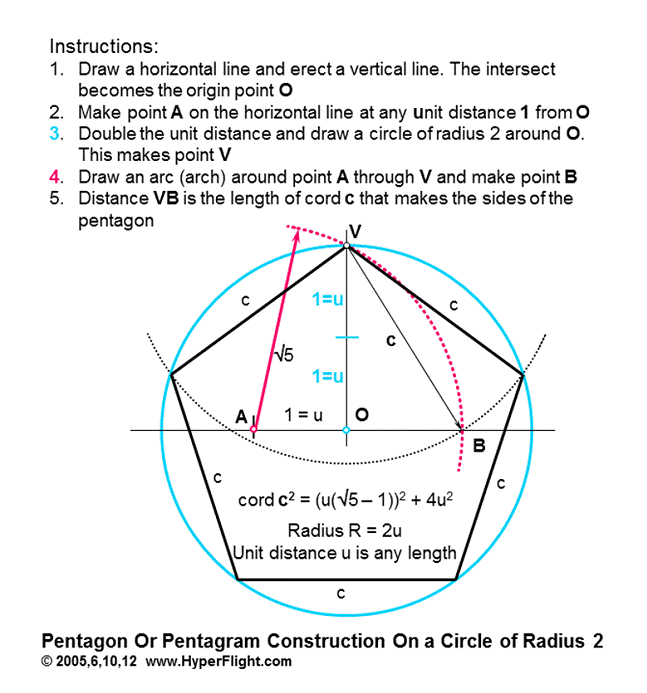 Construction (continued):
Construction (continued):
If
you want to construct the penta~ with a circle radius of your choice,
point A is one unit distance (one-half of the radius) away
from origin O.
When you divide a circle into exact fifths along the periphery you now have the template and:
Finish the pentagon by connecting every neighboring point and erase the circle. Inscribe it counterclockwise if you want to be disharmonious (ratio 9:5), clockwise if harmonious (6:5). (Cw and ccw makes a big difference — think enhanced modulo math. Ccw is acw for the Brits.)
or
- Complete the pentagram from pentacle by erasing the circle
- Make the five pointed star from pentagram by erasing the inside (smaller, upside down) pentagon. Also see pentagon tiling, further on
Make the pentacle by connecting every other (second) point. If you do it counter-clockwise, you will be doing it in the 8:5 ratio, which is harmonious, and you should not have a problem with that once you understand that the underlying pattern mechanics are clockwise — it's on the Venus page.
Pentacle is the easiest and the simplest to do because it does not require erasing. Does it mean it is the most fundamental?
Unit
distance
The
unit distance u
is the shortest distance used in construction of a particular star.
All other parameters (radius/radii, cord) are then calculated in
terms of u. This is new {Sep 2012}.
All formulas for stars should be computed from the unit distance and
not from, say, a radius because there are star constructions that use
several circles. In our example, the equation for the length of the
cord c in the above construction comes from two Pythagorean
relations and is quite involved:
but
for the five point hyperstar
cord c = 2u.
In either case, you can now substitute any distance for u and get the measures of the rest of star's parameters. There is more to this. Geometrically, the square root of five, for example, can be of any length and this length issues from the unit distance used in the construction of the SQRT(5). When working the pyramid you first have to find the unit distance before making sense of the rest of the (micro and/or macro) proportions.
Polygons
and stars
The
~gon identifies the point connections that go straight from one
point to the nearest next point on
a single circle — polygon
in general. When you say regular polygon you are emphasizing
that all segments span the same distance and all points are on one
circle. Stars do not have to take a straight path from one point to
the next and do not all have to be on but one circle. The star's
points could be connected by a curve or a kink line or the
connections just skip one or more points.
As
you go around the center from one point to the next, you might keep
turning in but one direction and then the star is said to be convex.
Regular polygons are always convex. 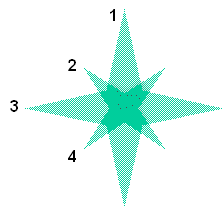 Sometimes
the points move inbound and out, particularly with multiple circles
holding the points, and you keep turning left and right when moving
from point to point. In such case the star is said to be concave.
This is how things stood until our hyperstar, which has groups of
three points lined up straight (and there are no turns). The
hyperstar is discussed in the right column. The hyperstar is not regular.
Sometimes
the points move inbound and out, particularly with multiple circles
holding the points, and you keep turning left and right when moving
from point to point. In such case the star is said to be concave.
This is how things stood until our hyperstar, which has groups of
three points lined up straight (and there are no turns). The
hyperstar is discussed in the right column. The hyperstar is not regular.
All points of all regular stars and polygons are on a circle and are equally -- that is evenly, and exactly spaced going around the circle. The best way of seeing it is that they have the exact fraction of a circle between them. However, only some stars are constructible exactly — see Perfect Families. As to the actual angles between points — see below, for these angles could be irrational numbers. (For now, ask yourself if a protractor can give you any irrational angle.)
Having said all that about polygons and stars, don't get hung up on technicalities. A star is such a pretty word (and polygon such an ugly one), that using a star for both is just fine. Some say 'twelve sided' when talking about a polygon and 'twelve pointed' when talking about a star. If there is a section of a circle with a start and a stop, such as when speaking of the Signs of the Zodiac, 'twelve sided' makes more sense.
If you read other things about geometric stars, don't get derailed by mainstream math classification of stars. Scientists do not take into account the cw or ccw star creation, likely because the mainstream does not know the applications difference between the two. (Harmony-disharmony enters here but there is more to it besides cw or ccw.) Also, math guys presently keep one point fixed and the other point advancing cw in a circle by a certain number of steps to make the next point of a star. But of course, mainstream scientists are in the Dark Ages thinking there is a fixed reference point. The Quantum Pythagoreans book gives all planets orbiting frequencies from which the stars are made and, gee, the Earth is orbiting while the cw or ccw point-to-point trace arises mathematically from that. Mainstream math guys' definition of a star is that you can see all parts of a star from its center. This is a great example of a definition of arm chair convenience because the Venus-Earth interplay makes a cool curlicue between points of a five pointed pentacle star and this does not match the scientists' definition of a star — so here is ours.
|
Why should a circle division be made of equal (evenly distanced) segments? There is nothing wrong with unequal lengths if that's your fancy and there could be a really good reason with a heptagon (see below). However, an electron's wavelength is proportional to the electron's energy and if several wavelengths of one electron were to fit (were to close) around the nucleus then they have to do so in whole multiples of the same distance. It's about the numbers (in a circle). |
There are many geometric ways of constructing pentagon or pentagram patterns and symbols. The construction presented here has the length of the side of the pentagon c the incommensurable (irrational) distance — that is, the measure of the side's distance is composed of an infinite number of digits (that do not repeat individually or as a group). Other constructions make the side c a rational distance, which is better suited for the Great Pyramid's purposes. In the pyramid, one half of the side of the base is (must be) a rational unit of measure, for such measure is executable and can become. (For transcendentals you may have to put a kink in that.) The connection between the five sided pentagon/pentagram and the four sided Great Pyramid is through the golden proportion, a subject that lets you understand how to draw and construct the Great Pyramid, and include the pinch on its side.
Angles in a five pointed star and how they relate to the golden proportion
 Determination
of pentagram's angles is easy — on the
interior or the exterior. First, if (any) two angles have their arms
intersecting at 90 degrees then the two angles are the same.
Determination
of pentagram's angles is easy — on the
interior or the exterior. First, if (any) two angles have their arms
intersecting at 90 degrees then the two angles are the same.
The central
(Egyptian) star below has 360/5=72 degrees between its arms. Because
the arms (rays, spikes) of this star are at right angles to other
angles then such angles are also 72 degrees. You will get to 108º
angle inside the pentagon with the subtraction of the 72º angle
from 180º (from a straight line). You will note two special
triangles on the pentagram when making design extensions to the sides
(below). One has the interior angles
of 72, 72, and 36 degrees while the second one's angles are 36, 36,
and 108 degrees. Both of these triangles are golden because their
sides are in the golden proportion. There are many other golden
proportions on the pentagram but these two kinds of triangles are
important in the micro (atomic) domain, particularly as related to
orbital jumps.
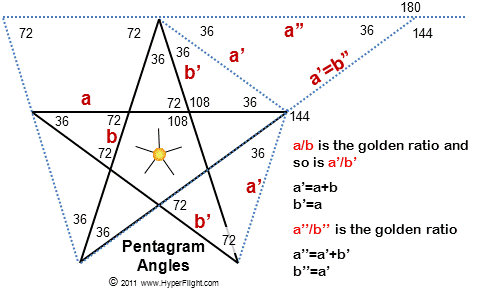
In multiples of
one tenth of a circle
All angles
internal and external to the pentagram or the five pointed star are
in multiples 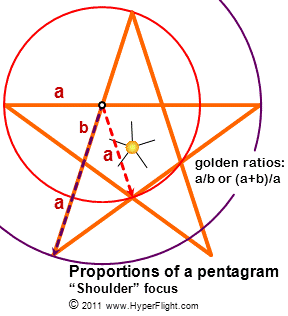 of
1/10 of a circle: from 36º on to 72º, 108º, 144º,
180º ... 324º, 360º. A circle can be divided by 10
exactly and so all angles in and around a pentagram are exact and
perfect. A pentagram, aka pentalpha, is a prominent symbol of the
Pythagoreans. It is said the pentagram is good for one's health, and
there could be something to it considering the golden proportions
that are all over the star. I think it is also likely the pentagram's
prominence is due to having an abundance of the number 10 while
adding a circular aspect to the many number 10
of
1/10 of a circle: from 36º on to 72º, 108º, 144º,
180º ... 324º, 360º. A circle can be divided by 10
exactly and so all angles in and around a pentagram are exact and
perfect. A pentagram, aka pentalpha, is a prominent symbol of the
Pythagoreans. It is said the pentagram is good for one's health, and
there could be something to it considering the golden proportions
that are all over the star. I think it is also likely the pentagram's
prominence is due to having an abundance of the number 10 while
adding a circular aspect to the many number 10  aspects
of the Pythagorean Tetractys. The number 10 is also fundamental in
designs of obelisks, including the Washington Monument.
aspects
of the Pythagorean Tetractys. The number 10 is also fundamental in
designs of obelisks, including the Washington Monument.
Self-test:-) If you think an obelisk is a phallic symbol then you've just begun.
The angle of 144º seems obscure (it's on the outside of the star) but it's the only angle you'll need if you want to draw a pentagram with a computer program the likes of 'Turtle,' 'Scratch,' or 'Logo.' The program would run like this (in pseudocode):
|
Pen Down [start] |
|
If these computer instructions do not mean much to you, you are doing well. First you want to create the geometric foundation — yes, in your mind, before resorting to a computer.
|
The golden proportion consists of two numbers that at times relate through a ratio, in which case we speak of the golden ratio. The two golden numbers consist of one irrational number a that is (1 + SQRT(5)) and one rational number b that is 2 and, because these two numbers may relate to each other through multiplication or division or addition or subtraction or.., they should not be reduced into a single number. Reduction into a single number severely limits the application of the golden proportion and that is one reason scientists like to reduce it as the Phi [scientists have reductionist tendencies – perhaps not a disease but it could be a handicap]. Reduction into one number hides other relationships the two golden numbers might have. |
The golden spiral
Golden spiraling
happens naturally in 2D or 3D as you observe the golden proportions
and figure out how you could grow them. Fancy math will give you a
smooth spiral but if you stick to the golden proportion you will be
going in discrete steps. (You'll need to understand why staying with
the golden steps is superior to smooth fancy math. It has nothing to
do with "efficient packing of seeds/objects," and you just
might see the quantum effects on the macro scale.) Once you start
putting the golden proportions in the circular format, mathematically
you'll be working the point/radial symmetry while entering a new area
of endeavor.
Pentagonal tiling
Also known in
general as tessellations, doing it in 5-fold rotational symmetry is
favorite of Dürer, Kepler, Penrose.. ..  All
pieces that make up sets for the five-fold 2D tiling have their
angles in multiples of 1/10 of a circle {July
2011}. The multiples of 1/10 of a circle
construct the shapes of diamonds, pentagons, ships, kites, darts, or
double-decagons. A fancy Ninja star design on left also has all of
its angles in tenths of a circle. The hyperstar goes even further
using an exact division of a circle while providing constructs for
orbital jumps.
All
pieces that make up sets for the five-fold 2D tiling have their
angles in multiples of 1/10 of a circle {July
2011}. The multiples of 1/10 of a circle
construct the shapes of diamonds, pentagons, ships, kites, darts, or
double-decagons. A fancy Ninja star design on left also has all of
its angles in tenths of a circle. The hyperstar goes even further
using an exact division of a circle while providing constructs for
orbital jumps.
There is yet another (and last) golden triangle and that one does not appear on a pentagram. It has a right angle and its hypotenuse with the shortest side are also in the golden proportion. This triangle is one-half of the Great Pyramid going across the mid face and into the center of the base. You can see it below on our Golden Eye design.
Pentagon
Dimension Priority: Diameter Dim or Point-to-point Length Dim
There is a dual
approach to a geometric pentagon star construction. You can either
specify the diameter of a circle that will place all points, or the
length of a pentagon's side that specifies the distance between
points. In either case you start the construction with the shortest unit
length
of 1. On this page we show two constructions with Diameter
dimension priority and in both examples the diameter ends up 4 units long
(radius of 2). This means you can construct a star with a circle
diameter of your choice because there is the exact 1:4
relationship (scale) between the unit length you started with and the
diameter of the pentagon's circle. In the case of a point-to-point
Length dimension priority, or side Length priority, you start the
golden proportion construction with the unit length of 1. When
finished, the pentagon will scale to the side length of 2.
Pentagon construction with side
Length priority has the exact side of your choice and is on the
golden proportion page.
|
A circle has many positive connotations. What would be the idea of dividing it? Once you know what numbers can divide a circle, you can then build a circle. Not [yet] from real things such as wood or metal but from waves. It turns out that the waves must have a particular wavelength count (a particular multiple of particular energies) before these waves are able to close in a circle -- and thus be symmetrical about a point. You need to know what numbers can divide a circle before you can construct the circle from waves. You might think this is something witches do, and you would be right, but an electron is a wave that wraps around the nucleus, too. There is (always) a bit more to this. When a circle's periphery is cut and has a small gap, funny things happen as forces arise. One could call this a circle corruption and in a way it is. Yet the forces that arise are not corrupting, for they attempt to close the circle and .. (think free energy). The making of a circle is also about taking a step from 1D to 2D. There, you will find the friendly transcendental number Pi. To round it off, you may want to learn more about the squaring of a circle, for it is about the straight and curving geometries. We did not forget the ancient Egyptians and use the example of the five pointed star as one of the steps in working the circle and the square. The golden proportion and Pi get very close to each other. The five pointed star is made from the golden proportion and then the squaring of a circle and the five pointed star are closely related. |
Ah, geometry
Not everybody likes geometry. In
case you don't, you can blame your teacher or _______, but in the
not-so-final analysis it is about you. Geometry is about movement and
placement in space, from an atom in your body to your ship as a
whole. Lots of geometry is in a plane and you have a good argument if
you say your head is not flat. So let me cut to the chase. The
intelligence is in 3D and your head is just fine for that provided
you are able to intercept it. Lots of free energy is in 2D and it can
be harnessed there once you figure out how to relate 3D to 2D. Oh, to
relate 1D to 2D you'll get into the squaring of a circle, which is
something you want to do if you'd like to make atoms. (Light is in 1D
and energy of an atomic electron cannot be in 1D —
it would leave the atom.) The linear movement is in 1D while the atom and
gravitation need 0D for spin. Your challenge, desire, need, or
necessity is to understand and work the Pythagorean tetra(ctys) of 0D
through 3D because that is how the universe is built and you want to
continue to be a nifty and smart participant in it.
Symmetry
in a five pointed star
Symmetry has appeal. It makes
things look nice but it could be difficult to move beyond that. There
are similarities with reflections in a mirror —
or refractions through a focus of a lens. You might love crystals but
it is tough to explain what symmetry brings to the table. Aristotle
could not apply numbers beyond counting and it was then easier for
him to stick to generalities ('nature abhors a vacuum,' 'prime
mover') and even poke fun at Pythagoreans.
There are two kinds of symmetries: even and odd. The even symmetry duplicates things about the (usually vertical) axis while the odd symmetry duplicates things by half-circle rotation about a point at the origin, which is the center of the circle used to make the star. Symmetries issue from geometry (and geometry issues from numbers). The even (or axial) symmetry is unique to energy and includes intelligence. Esoterically it is the head of the Sphinx while the empty space between the Sphinx' front paws is the (virtual) line of the axis of the even symmetry. The odd (or point) symmetry is unique to charge and matter. The even symmetry is inclusive while the odd symmetry is exclusive. Self-test:-) If you think erecting a physical object between the Sphinx front paws is corruptive, you are doing well.
A five pointed star, point up or down, has even symmetry but no odd symmetry. You could also have heard of 'rotational' symmetry. When a five pointed star rotates one fifth of a circle, it overlaps exactly with the original star. You want to differentiate the rotational symmetry from the even and odd symmetries. Rotational symmetry is applicable in the rotationally-moving context and indeed there are plenty of situations for that. I like to call the even and odd symmetries the placement symmetries while the rotational symmetry is one of the movement symmetries. Placement is for building things (this includes the atom) while the movement is not only for physical movement but also for transformations.
Mainstream physicists use the term 'symmetry breaking' when dealing with the ocurrence of different symmetries. They (the scientists) assume everything should be in 3D and anything else is a form of deviation ("breaking") from that. This is very stupid. The fundamental thing to look for is computability. If the system is computable, it will happen. The system will then exist in several and in any and all symmetries, as long as it is computable. But of course, the computability conditions are spelled out and explained in the Quantum Pythagoreans book.
This talk about symmetries becomes introductory once you begin to appreciate that the (law of the) conservation of energy is based on the conservation of symmetries. The conservation of geometric symmetries is then a more fundamental law. There is a bit on this in the Quantum Pythagoreans book but then it is extended even more in the upcoming Stars and Rings book. What? Who needs cables?
|
|
|
The radius measure of 2 (diameter of 4) in our pentagonal construction on the left is the outcome of using the shortest applied distance as the unit 1. This is not because you couldn't divide by two (you can -- and work with ½ as the distance OA, for example), but if you construct other structures such as the the Great Pyramid with the shortest distance as the unit 1, you will always be in sync with your numbers from one structure to the next. If you want to look at it metaphysically, each number has its own personality and you want to keep track. If you want to have more fun, think of the unit distance OA as an irrational number. Even Euclid did not think of the number 1 as just a counting number.
|
|
|
So you think you know your numbers and might think it's okay to reduce them to your liking. But if you construct the Great Pyramid with the golden numbers and use the shortest distance as the unit 1, you will arrive at the pyramid's base as having the side length of 4. The base of the Great Pyramid is then 4 times of some unit of measure. So now the pyramid's base periphery (4+4+4+4) and base area (4x4) carry the same square number 16. You see, if you reduce the numbers and think of the pyramid's base as having the unit length of, say, two, the base periphery would have eight units of length but the base area would be but four (square) units. If you do not reduce the numbers you can think of the number 16 in the context of acceleration (unit of measure per time squared) and derive the unit of length that is most appropriate for this planet [yeah, it's a foot]. Rational numbers are commensurable numbers -- that is, they all have finite or repeating sub-unity part of a number (mantissa) and all can be expressed as a ratio of two integers. Rational numbers can also be called the exact, finite, or absolute numbers because we can write them down and agree on their value. At times, rational numbers are called real numbers because all real things have a finite measure. Rational numbers happen when we ratio two integers. All mainstream mathematicians define the rational number as the ratio of any two integers. So, a mainstream math guy would say, "Of course the rational number is a ratio of two integers -- it is defined that way." Yet, you really do not want to be mainstream and acquire but an encyclopedia knowledge of the world. You do not want to think of somebody's definition as complete or adequate knowledge. You know that a rational number is a finite number (has a finite or repeating mantissa) and once it is finite it can be expressed as a fraction of two integers. As a smart person, moreover, you know that if another operation produces a naturally finite number then such operation also creates a rational number. The circumference of a circle is a transcendental number. Many of circle's round segments (arches) are transcendental numbers and their straight cord could be an irrational number -- and both of these numbers have an infinite mantissa (infinite precision). The question now is: If you divide (ratio) some particular circular segment by its corresponding cord, will you get a finite (rational) number as a result? |
|
Some Pythagoreans view the number two as a problem number because it "divides the unity." Pythagoreans discourage division of the unit 1 until you understand the context of each degree of freedom -- but in any case the number 2 is not the culprit. (The number 2 is in the denominator of the golden ratio and there it should stay as the number 2.) As you get familiar with this site the sub-unity will become applicable to atomic orbitals and hence the number 1 is the Great Divide between the macro-cosmic and micro-atomic. [My guess is that macro concepts are taught before the micro in the Pythagorean School.]
Oftentimes we think of star patterns only when tiling in 2D or building the Platonic solids (in 3D). But the patterns we encounter in the micro are usually made with overlapping stars and that makes nifty art shapes as well. The overlap comes from the inclusiveness of waves.
|
|
Large-print format is becoming affordable. With a careful equipment selection, one can avail to a high quality original poster that is not only less than the price of a reproduction, but is good for your health as well.
Just about ready (second picture).
|
|
Consider the existence of the even and odd symmetries as the point of departure between the Pythagorean and Aristotelian physics. Pythagoreans continue basing new concepts on numbers and then the even aka twofold symmetry issues from and relates to the number two (and the feminine). Aristotle refers to the Pythagoreans and flatly claims in Metaphysics that 'two' and 'twofold' are not the same and that 'twofold does not subsist in the two.' (Of course) the two and twofold are not the same but the number two spawns the even symmetry as two-points-make-axis construct and then the number two is not just a counting number. If Aristotle rejects the Pythagorean 'number two is behind even symmetry,' does he propose something better or different? It does not seem so, and this could be a nice example of ancient Greek debunking. Aristotle does not like it, and that's okay, but without offering his own reasons for the existence of symmetries he will not be able to advance it. Sure enough, we don't hear from Aristotle on symmetries. Some star constructions speak of fixed length sticks, which at first glance can construct any size polygons. Here is where the executability of angles comes up. In space, the irrational angle is constructible only approximately and only some angles will be actualized – think snowflake formation. Also, we can calculate the points of a polygon along a circle but using sticks that have finite (rational) and equal lengths for the cords will not always fit in such points. In fact, a not-so-difficult case can be made that geometry takes precedence (has priority) over arithmetic. [If you are a scientist, you may think of Emmy Noether who ignored the nature's beauty of snowflakes and made simplifying assumptions about space that proved the 'ignorance is bliss' postulate – for in her world everything is reduced and snowflakes and crystals don't exist.] You can calculate the area of any polygon by taking the area of the triangle and multiplying by the number of sides. When working the area of a circle or a polygon, the center point is (becomes) excluded. (If you are metaphysically inclined, think Isis looking for all parts.) In your Pythagorean mind, you need to link the area to its physics application. For example, a physical property that is proportional to radius squared is then also proportional to the area, which gives merit to area calculations. This is bigger than it seems. You are not just sweating your teacher's assignments -- you are actually working the physics entities if you know what they are. |
One other
Penta~ construction
This one comes
from Yosifusa Hirano of 19th Century
Japan. It is elegant and also constructs the pentagon or pentacle on
radius 2.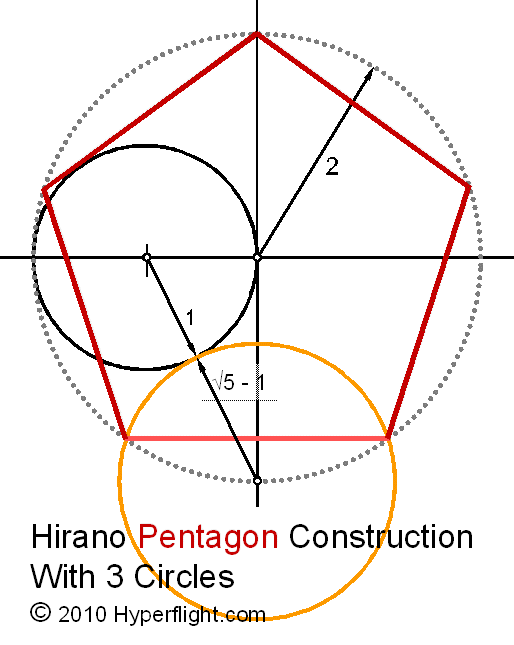
The angle
of 72 degrees
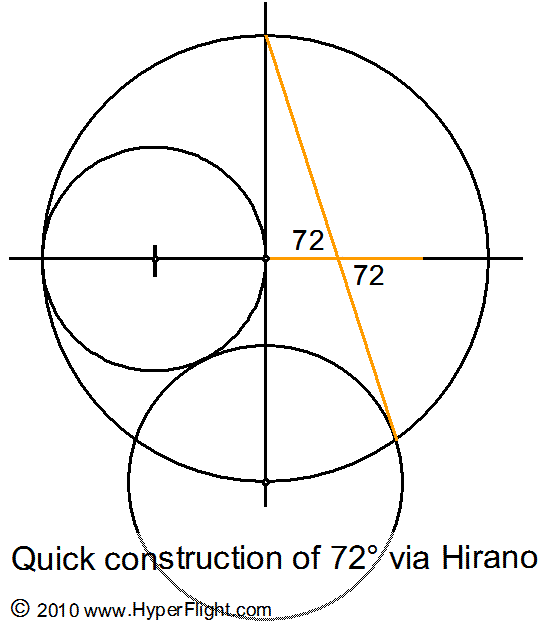
If you think the
construction of a 72 degree angle above is special, consider it the
exact one fifth of a circle rather than a number with some magical
properties. The angle of 72º is 360/5 but the number 360 is arbitrary
to begin with. Geometric one fifth of a circle gives you the exact
division of 2Pi and you now have the exact division of a transcendental
number — something your computer cannot do. Yes, the arithmetic
division of a circle by a whole number (or any rational number) must
use the circumference or an area of a circle, which is based on the
number Pi having an infinite mantissa — and the arithmetic
result is never exact because the result has an infinite number of
nonrepeating sub-unity digits. The modified Hirano construction below
begins to work the transcendentals in the square-a-circle context.
Visit the proofs page.
"All pentagram angles are arithmetically divisible by nine."
"What?"
"Or by four."
So, what's the big
deal if the number 360 (degrees in a circle) is no big deal?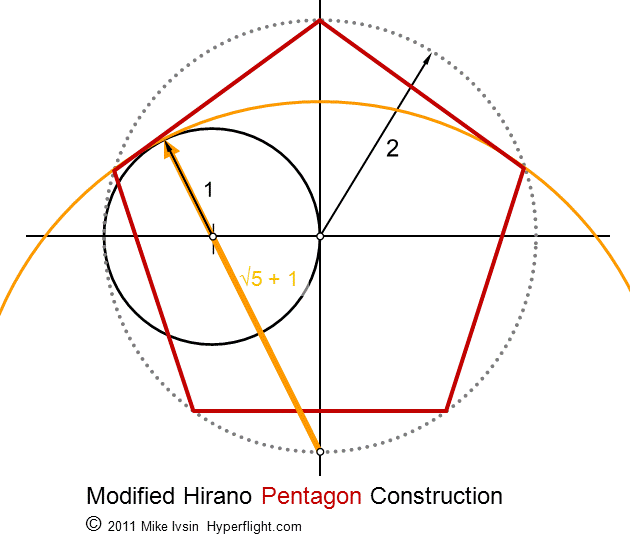 If you line up all angles from the pentagram: 36, 72, 108,
144, etc. and sum their individual digits you will always get 9. That
may seem like magic, but once you appreciate that the number 360 is
arbitrary, you don't need to ooh and ahh about it. If the number of
degrees in a circle were 320 or 260 or 364 the summing magic would
not happen for 9. The circumference of a circle is 2Pi and putting in
a number to stand for degrees is purely a practical consideration. In
the case of 360, this number is 4x9x10 and now, because the angles of
a pentagram are in tenths of a circle, the number that is left is a
multiple of 9 (and 4) and so it will be always divisible by 9
(or 4). All numbers divisible by 9 have their digits sum up to 9
(modulo 9 — thank you, Gauss).
So, always work with fractions of a circle (or fractions of 2Pi) even
if the numerical sub-unity pushes your right brain into infinities.
There is plenty of real magic left in this subject, particularly if
you get into the squaring of a circle.
If you line up all angles from the pentagram: 36, 72, 108,
144, etc. and sum their individual digits you will always get 9. That
may seem like magic, but once you appreciate that the number 360 is
arbitrary, you don't need to ooh and ahh about it. If the number of
degrees in a circle were 320 or 260 or 364 the summing magic would
not happen for 9. The circumference of a circle is 2Pi and putting in
a number to stand for degrees is purely a practical consideration. In
the case of 360, this number is 4x9x10 and now, because the angles of
a pentagram are in tenths of a circle, the number that is left is a
multiple of 9 (and 4) and so it will be always divisible by 9
(or 4). All numbers divisible by 9 have their digits sum up to 9
(modulo 9 — thank you, Gauss).
So, always work with fractions of a circle (or fractions of 2Pi) even
if the numerical sub-unity pushes your right brain into infinities.
There is plenty of real magic left in this subject, particularly if
you get into the squaring of a circle.
|
|
Two pentagons
make a decagon, a regular ten pointed star
 A
regular pentagon made with the Hirano method can be used to easily
make a regular decagon — an exact ten-point star. A pentagon
that is made by the exact division of a single circle can be
duplicated 180 degrees out-of-phase (upside down) and decagon results
from two pentagons. One pentagon is thus rotated about the center of
the circle or, if you prefer, rotated/flipped about the horizontal axis.
A
regular pentagon made with the Hirano method can be used to easily
make a regular decagon — an exact ten-point star. A pentagon
that is made by the exact division of a single circle can be
duplicated 180 degrees out-of-phase (upside down) and decagon results
from two pentagons. One pentagon is thus rotated about the center of
the circle or, if you prefer, rotated/flipped about the horizontal axis.
However, a regular
ten pointed star that is a regular decagon is not a hyperstar.
(Hyperstar is discussed in the right column.) 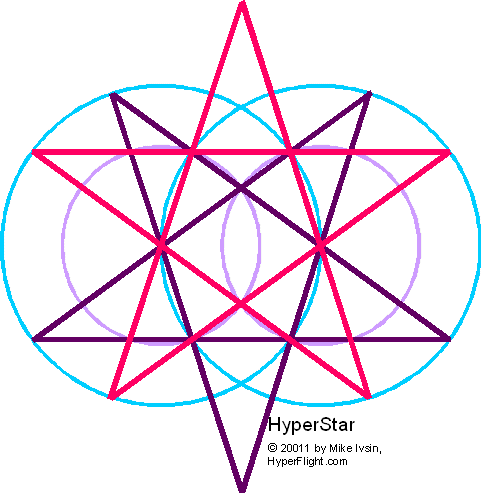 While
both stars are created from two regular five pointed stars, a
decagon is always convex. A hyperstar has some straight segments
spanning three points. A decagon has its points on a single circle. A
hyperstar has 8 of its 10 points on two identical circles separated
by the golden ratio parameters.
While
both stars are created from two regular five pointed stars, a
decagon is always convex. A hyperstar has some straight segments
spanning three points. A decagon has its points on a single circle. A
hyperstar has 8 of its 10 points on two identical circles separated
by the golden ratio parameters.
|
[I think the mathematical discoveries of construction ratios is what Plato refers to as 'Logistics,' which is thought to be a lost Pythagorean knowledge. In the case of a pentagon Diameter priority the ratio is with square numbers (1:4) because we go from 1D (unit length) to 2D (circle). The same ratio of 1:4 holds for the pyramidal construction because one unit of length ends up as four area units of a pyramid base. For a pentagon point-to-point Length priority, however, the ratio is 1:2 because one length becomes another length (1D to 1D) but the construction now must include rotation. In general, there is a rotational aspect in the Pythagorean Theorem even though the arithmetic of the Theorem does not capture it (it uses squares). Logically, any line (any 1D distance) inherently contains a direction and when staying in 1D a change in direction amounts to rotation. Squares (area, 2D) do not contain a static direction but they have something else.] |
|
Every time you double something – think octave. Every time you halve something – think node (or fit) for standing waves. Every time you rotate by 45 degrees – think transformation. Every time you rotate by a right angle – think.. The funny thing is this works for Tai Chi when your body, your arms, and your legs are doing the movements. Geometry and movement is about your health too. |
Harmonious ten
pointed star
The star below, if
drawn counterclockwise, is classified as a (10+7)/10
star using my method that is (x+y)/x in general {while y
is between 1 and x — that is, x>y>=1}.
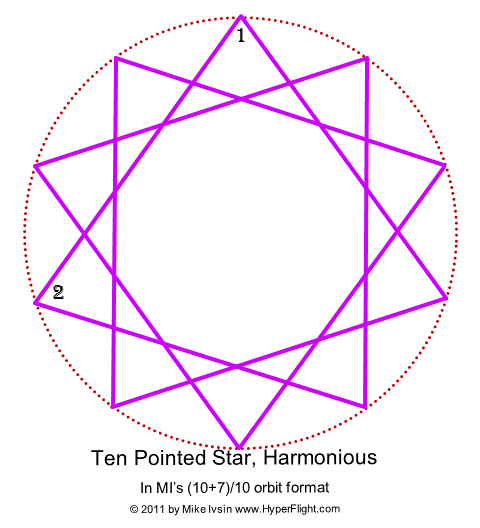 The
decagram star looks nice — it is unicursal, is regular during
construction (advances by the same angle), has parallel sides and is
harmonious. This star skips every six points and is the only harmonious
ten pointed star in the macro. (Decagon and all other ten-point stars
are not harmonious, cw or ccw.) The Pythagorean style rationing
(really proportioning) method (x+y)/x as well as the
corresponding musical harmony or disharmony is explained in the book,
and you'll know why the proportioning approach presented here is much
more useful than what the mainstream puts out. You noted x and y
are integers but if x and y are the golden
numbers then (x+y):x
is the golden proportion — and enter both the micro and the
macro. (Rationing is not commutative because A/B is not B/A.
Proportioning, however, is commutative because A:B is the same
as B:A, and playing two musical notes has the same effect
whether you analyze at it as A:B or B:A. Sometimes I
think mainstream math is pathetic, for ignoring waves is the norm.)
The
decagram star looks nice — it is unicursal, is regular during
construction (advances by the same angle), has parallel sides and is
harmonious. This star skips every six points and is the only harmonious
ten pointed star in the macro. (Decagon and all other ten-point stars
are not harmonious, cw or ccw.) The Pythagorean style rationing
(really proportioning) method (x+y)/x as well as the
corresponding musical harmony or disharmony is explained in the book,
and you'll know why the proportioning approach presented here is much
more useful than what the mainstream puts out. You noted x and y
are integers but if x and y are the golden
numbers then (x+y):x
is the golden proportion — and enter both the micro and the
macro. (Rationing is not commutative because A/B is not B/A.
Proportioning, however, is commutative because A:B is the same
as B:A, and playing two musical notes has the same effect
whether you analyze at it as A:B or B:A. Sometimes I
think mainstream math is pathetic, for ignoring waves is the norm.)
Not done yet
There exists
symmetry about one point called the point symmetry (or odd or
radial or rotational symmetry) [masculine]. There also exists
symmetry about two points called the even symmetry (or axial
or twofold or mirror line symmetry) [feminine] — the two points
making an axis by which the original image rotates. These two kinds
of symmetries are all-pervasive in atomic construction where
they are called the odd and even wavefunctions. Yes, everything is
coming up numbers. Now, how would you marry these two symmetries?
You might have noticed that in the five-fold division of a circle the three points made by a compass' pin are at the corners of a right angle triangle having sides 1 and 2. (A pin of a compass centers the radial symmetry [masculine].) It is no coincidence that the Great Pyramid's Grand Gallery has the vertical height (rise) of 1 and the horizontal length of 2 while the Trough is the hypotenuse spanning the distance of SQRT(5). (This also establishes the unit length 1 of this pyramid.)
Is it a coincidence that to define Pi we need distances 1 and 2?
Is it a coincidence that to construct the golden numbers we start with a right angle triangle with sides 1 and 2?
There is more
to 5
It is very easy to
get excited about the number 5 and begin to associate each of the
five points with other things. This is a Pythagorean site and we love
the number five but Pythagoreans also know that using numbers for
counting is introductory to the power of numbers while
correspondences are about the elemental — that is
differentiating, power of numbers. The five discrete elements in
Wicca and Tao are fine, yet the visual-geometric imagery based on the
Penta~ is about the infinity (irrationality) of the golden
proportions stemming from the square root of five. With the
golden numbers you construct many shapes that extend the Penta~
beyond counting. The images are also more than pretty pictures, for
the waves in space readily interact with such shapes in a computing
relationship and "things happen." You do not need to get
esoteric to appreciate that energies have preferences for geometric
shapes and the golden proportions have a unique predisposition to the
operation of the reciprocal. (Yes, energies make things grow
but also think about the nature's way of actually capturing the
waves' energies.) 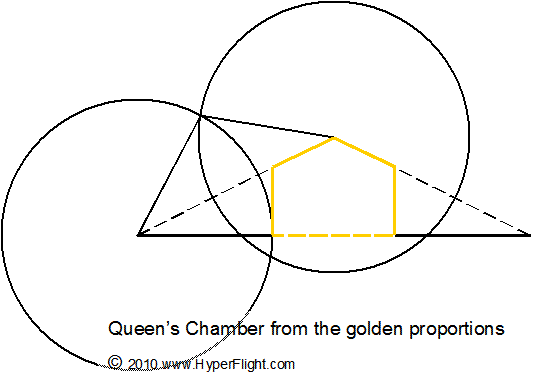 So
it is nice to recognize the golden shapes around you even though
neither the star or the number five jump out at you. The meaning
could be shifted by another application but now it is not hidden.
[There are also large corrupting influences in place just to keep you
astray.] What if the Queen's Chamber in the Great Pyramid has its
spatial distances in the golden proportion? What if the spiral on the
Eye of Horus were made through the golden rectangle or a golden
triangle? How can you visualize the golden
ratio in financial terms?
So
it is nice to recognize the golden shapes around you even though
neither the star or the number five jump out at you. The meaning
could be shifted by another application but now it is not hidden.
[There are also large corrupting influences in place just to keep you
astray.] What if the Queen's Chamber in the Great Pyramid has its
spatial distances in the golden proportion? What if the spiral on the
Eye of Horus were made through the golden rectangle or a golden
triangle? How can you visualize the golden
ratio in financial terms?
|
Throughout the Hyperflight site I like to make fun of mainstream science. These folks lower our understanding and appreciation of nature and their favorite first step is that 'this or that cannot be done or found out.' The best modern example is Einstein and I don't know of any of his concepts that are correct: This includes the special and general relativity theories (stemming from his inability to determine absolute motion/rest); photonic work function (a photon puts no pressure on a mirror); Brownian motion (molecules vibrate in place); and energy-matter mechanics (not reversible, i.e., nova or supernova). Errors of omission and commission are also applied to corrupt the reality around us. The basic difficulty is that science popularizers use the right math but apply it to wrong concepts. It may take a while to "get to the bottom of this" and what really helps is that equations cannot make wrong concepts right, and therefore are suspect. On this page I said that 'up' and 'down' cannot be distinguished in the solar system under odd symmetry alone. Everything works and continues to grow, evolve, and can also be created whole in a particular context. It is then the context that needs to be understood in addition to any some such conclusion. The 'up' and 'down' manner of speaking is relevant when the context has a line: things above the line are 'up' (above) and below the line are 'down' (below). However, orbits and orbitals and spin in general have a point as its construct of rotational/spinning existence and it is then appropriate to say that when dealing with point symmetry there is no fixed 'up' or 'down' because there intrinsically is no (fixed) line. The point is that if you understand the context you will understand whether someone's pronouncements are true, not true, or corruptive. For example, ignoring 0D (a point) as the fourth dimension of freedom -- which provides a movement construct just as 1D, 2D, and 3D do -- is corruptive because it does not recognize the spin/orbit that accounts for 99% of the moving energy found in the universe. There are several ways of getting to the truth, too. Geometry is one. Tarot works nicely and in this case it's The Wheel of Fortune card. Tarot has four suits, which stand for .. (your brainwork). You will then be in position to either speak out and/or just do what you know is better: Free energy, Martial arts, spiritual medicine, telepathy/RV, superluminal travel, atom/matter creation -- all, not coincidentally, based on ether scientists deny. Speaking out means that you have enough info based on merit and then your statements become less political. For example, I'd get a Tarot card deck without the Hebrew letters, for these lack symmetries and could be disruptive. (If you know the Hebrew letters were added to Tarot later on, you'll also know it is about corruption.) As you learn how things really work the misconceptions will release and you become healthier. After reading a book on the history of the Chinese philosophy that weaves through the Confucian, Taoist, and Buddhist pursuits over 2300 years there, it seems the Chinese never got to the understanding, and then the differentiation, of the symmetries. Yet I would not relax too much after this. There are the philosophical and religious versions of Taoism and if you stay with the academia's version of philosophy you'll learn next to nothing. Once you get to the religious side you will read a lot about circles and spirits and demons, about keeping centered (weighed) in a point and having light crystallized -- but all this is pure alchemy and it takes some dedication for the ideas to work their way through (just as you would do with the ancient Egyptians). While the Chinese did not push the three philosophies/religions into the objective realm we call science, the Chinese pursuit in the improvement of the individual's mind-body yielded Tai Chi with most significant implications -- and leaving a formidable gap for "the West." Wang Fuzhi (b. 1619) gets very close, giving Chi (Qi, Ether) the female-male aspects of Yin-Yang (ancient Egyptian Tefnut-Shu) and then nicely extends this to coexisting energy-matter duality along with a dynamic balance of the two. Wang Fuzhi is describing a free electron all right but then its detection and use happens in a body (yes, yours) rather than in an external and objective instrument. (Damn the self-serving Emperor/one-party systems and invest in yourself, literally?) Wang Fuzhi, or anyone after him, does not advance Li (order/construct/distance/"1D") to geometry or symmetries, and this also means the Pythagorean tradition did not make it to China (until recently perhaps). We can then also say that the Taoist five pointed star of the elements is indigenous to China (could've been discovered in more than one place) and testifies to the universal power and utility of the five fold division of a circle. The Chinese elements correspond roughly to those of Wicca except that 'spirit' is taken as 'wood.' This seems strange but think of wood as the circles of tree rings, too. This also gives you an idea how "hidden" Chinese alchemy is. (Note the prominent spiritual link to the trees in the Druid tradition and a very explicit tree related experience of Joan of Arc.) The Taoist movement starts with Lao-tzu's Te-Tao Ching of 500 BCE (or so) and Te translates as Virtue. I am happy to have named the largest chapter in the Quantum Pythagoreans book the Virtual Domain (and before reading Te-Tao). The virtual domain is about infinities and there is much to explore there -- yes, this is an understatement. (One can also destabilize in John Nash fashion. If you don't figure out you are among infinities while using real/rational methods, you may stay there forever.) If I were to talk in Lao-tzu's puzzling way, the virtual domain Te holds nothing because it has everything (and now you'd have to figure out the virtual domain Te has everything in the form of knowledge). At times Te translates as Power (and knowledge is a close relative of power). Lao-tzu described Tao in the most general way. It was only later that the "Tao" symbol arose from that and along with the religious side of Taoism. But of course, the Tao symbol is but the Chinese version of what the infinite Tao is or could be used for, including the label of 'Tao.' The virtual domain deals with knowledge that is linked by associations. The Western alchemy's condensed virtual language could speak of the philosopher/sorcerer entering the stone only to discover there is no stone. Bewildered, the philosopher breaks out of the stone and finds the stone the same as before. He cannot break into the stone and yet he does not have to break up the the stone to reenter it. The philosopher's stone can be had -- but not physically. Yikes! Here is s'more on stability via organization. |
|
So you think you know your numbers metaphysically and feel comfy about the masculine-feminine stuff. You might be dividing by 2 and think it feminine. Not so. Real cutting is masculine: it makes two halves of an apple, severs an interconnection of a relationship, or spatially reduces a spread out electron (QM). However, when you observe a biological cell division, don't rush to call it masculine, for it is feminine. You'll have to get into symmetries to understand this. Meanwhile, don't make the silly mistake of equating masculine with a man and feminine with a woman -- unless you want to give up on one half of your brain. Oh, and think about The One. |
|
Analytically attacking all three major pyramids at Giza as one layout can earn you a label or two, but on this site Jiri starts with a square and then looks for the golden proportion – and gets very, very close to the actual measurements. Ready to bury the Pharaohs someplace else? |
Some basic geometry. From a square angle to a square
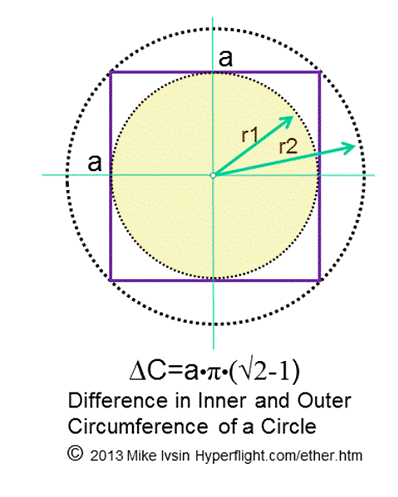 There
does not appear much we can do with a square. A square is pretty,
has a lot of symmetries, but that's about it. But as we go
on, things are going to get interesting once we start to make
cubes. Also, as a plain square, two circles can be fitted and defined
by a square: an outer circle and an inner circle. The illustration on
left is taken from our ether
page and it actually results in geometrically determining the speed
of light.
There
does not appear much we can do with a square. A square is pretty,
has a lot of symmetries, but that's about it. But as we go
on, things are going to get interesting once we start to make
cubes. Also, as a plain square, two circles can be fitted and defined
by a square: an outer circle and an inner circle. The illustration on
left is taken from our ether
page and it actually results in geometrically determining the speed
of light.
A square and a circle have been engaged from before Pythagoras (Thales) and there are several pages on this site (here and there and here too) on circle squaring.
Pythagoreans love square numbers. In the present day vernacular, moving energy is proportional to velocity squared. Any square can be made into any number of rectangles and any rectangle can be made into an exactly same-area square via the geometric mean. Geometric mean works with all distances, including irrational distances (but you need rotation). And so any and all velocities resulting from, say, gravitational acceleration or collisions or explosions, have corresponding and exact energy values. Any square (any amount of energy) can be divided into as many squares as you want — and so the energy of one moving object is conserved exactly even if the object is broken up into many other objects.
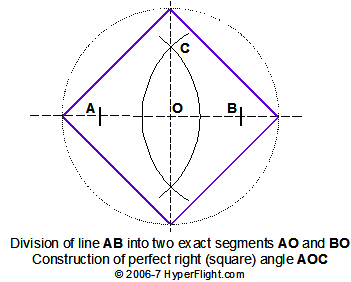
Here is a simple yet powerful construction that
1) Divides any distance exactly
in half;
2) Erects the perfect right and
square angle (making the Cartesian Coordinates); and
3) Makes a true square using any
circle centered at O (at the intercept of horizontal and vertical
axes that are the coordinates). A square is also a four pointed star
Only straightedge and compass are needed. (Straightedge is an unmarked ruler.)
Both arcs (arches) have the same radius.
Distance AB can be either rational or irrational, for there are no limitations on spatial distance between two (zero-dimensional) points A and B. Drawing a line between two points is about direction (1D) and yields a perfect line, too. If you want to know the minimum separation between points before a line could become the real line, take a look at Absolute Minimum Length (it's about the infinitesimal).
If distance AB is irrational, should it be dashed? If so, why?
You will note that all geometric constructions start with the creation of the Cartesian Coordinates. Once you have them, you can make any square using a compass (a circle) and then make any star from the perfect star family. A square, then, is inherent in all star constructions.
A square is feminine and a circle is masculine. Some people get into spirituality and claim a circle is feminine because it is "rounded." That is how you can tell a beginner. Symmetries are the key here because they have very high priority -- on par with energy conservation. Ancient Egyptians, Native Americans, and Chinese have no problem here. Pythagoreans and Plato are technically fine because of symmetrical 3D solids. Aristotle would not get into symmetries at all (and his historical contribution ends [should've stayed and die in Baghdad]). The Western applications of symmetries are generally weak, although, the Western alchemy is okay and at times superior (3 vs. 4).
Three pointed star
Construct
the perfect triangle on a circle and another triangle on a
semicircle –
in three steps
Triangle as a
logical and mathematical construct
Because
three-pointed and six-pointed stars are geometrically perfect they
can be used, circled, as a symbol for 3 or 6 wavelengths wrapping
around the nucleus. However, a hexagon and hexagram reduce into a
triangle under modulo math for harmonious ratios and do not manifest
in orbits (macro) — that is, showing a six-pointed star with two
circles does not reflect nature.
A hexagon is also prominent in free energy work. Hexagon is full of different symmetries and, for better or for worse, enables rapid transformations or projections. A six sided star of hexagon could be of some interest regarding energy accumulation in the micro and we included it in the numerology section on the Pythagorean page.
Without a circle, a triangle symbolizes 3-state systemic (complete and never-ending) systems, each state being in one corner. Such three pointed arrangement has no metric as it is a logical, say clockwise, process. (Some systemic processes call for quaternaries — think ancient Egyptians.) For Pythagoreans a triangle provides bounds for the ten dots of Tetractys (a triangular numeral 10), which also becomes one facet of a tetrahedron (projection from the apex [or from your eye]). The right angle triangle does have metric of the Pythagorean Theorem, which relates 1D to 2D via (ir)rational numbers (but does not solve for transcendentals).
There is a very special place for the golden triangles. Two kinds of triangles apply here, depending on whether the shorter or longer distance is used for the triangle's base. Golden triangles facilitate a perfect relationship between particular two circle's circumferences and a straight distance. Yes, this is the fundamental reason for the existence of particular atomic orbitals, which is driven by the exchange in the electron's 2D and photon's 1D energy {Feb 13, 2011}. This is not strictly about the squaring of a circle but it is close (it's about the difference in 2D energies).
Differentiate
by 3
Finally, there is
an aspect to the number 3 as the fundamental qualitative
differentiator of nature. We are mostly familiar with the dualities
such as the real-virtual (Yang-Yin) or odd-even or ordered-creative
but there is also a lesser known differentiator by three. Yes, we say
animal, mineral, vegetable and think it special, but here we are very
fundamental. Pre-atomic, I'd say. So much so the crop circles are
worth studying just for that. [I would not go inside a crop circle
for more than a few seconds when the circle is less than a day old
— it is about the 3D energies.] Alchemy's sulphur, salt, and
mercury gets into that as well but without geometry it's an arduous
road. The Quantum Pythagoreans book explains what is at each
corner of the Tetractys and that's what it's about.
When you see a triangle with some symbol in the center (a dot, an eye, dragon), take such symbol into 3D of the apex of a tetrahedron to see if it means something to you.
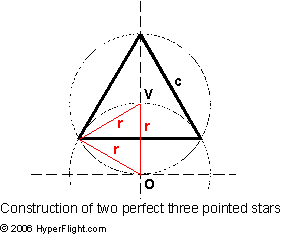
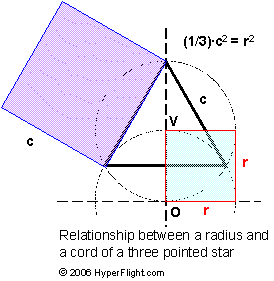
- Draw
horizontal and vertical lines. The intersect is the origin O
- Draw a
semicircle of radius r around O. This makes point V
- Draw a circle around V of radius r
Instructions:
Now that we
divided a circle into exact thirds, you can make a three pointed
("Mercedes") star or a three sided star of a perfect
triangle. In the illustration the larger triangle divides the circle
with three exact cords of length c
for a perfect three pointed star.
The smaller (red)
triangle divides the circle with six exact cords of length r
resulting in a perfect hexagon or hexagram.
You can verify
(using the Pythagorean Theorem) that the relation between the cord c and
cord (radius) r is:
c2
= 3·r2
What physical
entity is proportional to r2?
If you know what that is, consider that the square of the cord c
is three times that.
|
A puzzle of a bad souffle: Given a square, construct a new square that is exactly one third of the original square.
|
||
A six sided
star, a hexagon, is prominent in virus structures. 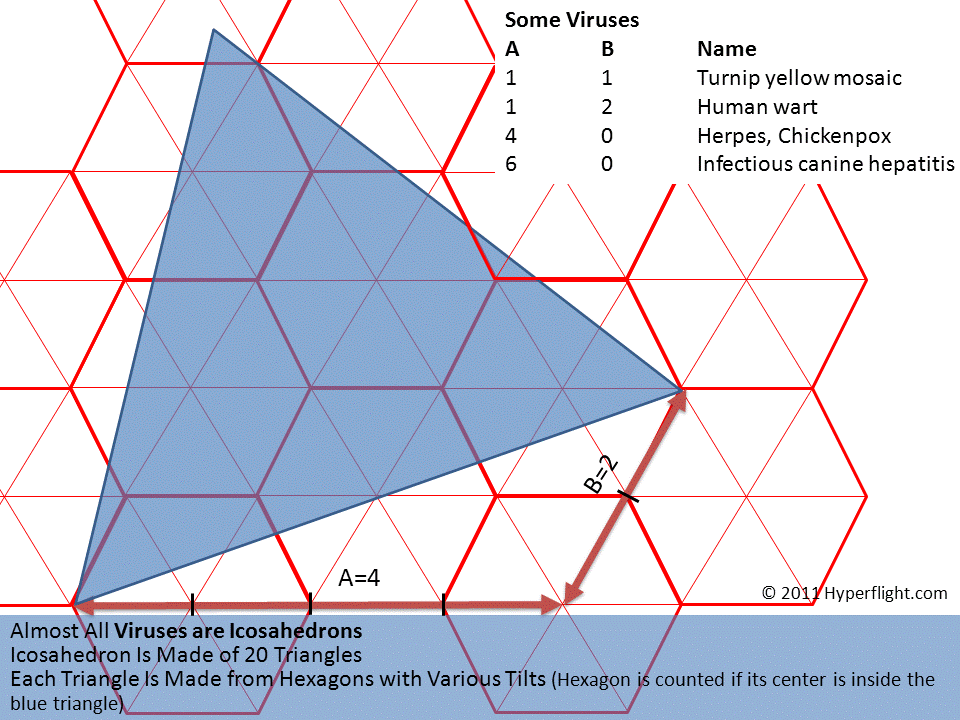 Hexagons
are partioned into a six-triangle grid, which serves -- through a
geometric relation -- to identify almost all viruses. This is a
complex topic. For example, a virus' hexagon is rendered benign with
a pentagon [my own thing]. The overall structure in 90+% of viruses
is icosahedron.
Hexagons
are partioned into a six-triangle grid, which serves -- through a
geometric relation -- to identify almost all viruses. This is a
complex topic. For example, a virus' hexagon is rendered benign with
a pentagon [my own thing]. The overall structure in 90+% of viruses
is icosahedron.  Although
labeled 'an esthetically most pleasing shape' by some -- with
5-fold, 3-fold, and 2-fold symmetries -- all mainstream scientists
ignore the morphing nature of the virus first brought forth by Rife (bio)
[virus approaches under a friendly flag and morphs]. Because the
current work on viruses discloses but the stained (i.e. dead)
viruses, the mainstream is still way behind Rife. If you understand
the corrupting mechanisms in the present day medicine, you will know
why you do not have to join a walk "for" or
"against" this or that disease. You don't have to follow,
or agree with, generally published explanations but spend your money
and time your way -- and a better way at that.
Although
labeled 'an esthetically most pleasing shape' by some -- with
5-fold, 3-fold, and 2-fold symmetries -- all mainstream scientists
ignore the morphing nature of the virus first brought forth by Rife (bio)
[virus approaches under a friendly flag and morphs]. Because the
current work on viruses discloses but the stained (i.e. dead)
viruses, the mainstream is still way behind Rife. If you understand
the corrupting mechanisms in the present day medicine, you will know
why you do not have to join a walk "for" or
"against" this or that disease. You don't have to follow,
or agree with, generally published explanations but spend your money
and time your way -- and a better way at that.
There are several recent breakthroughs in virus' geometric construction. The geometric steps in virus' formation are: diagonal projection of a cube resulting in a hexagon; slicing-and-projecting a cube grid resulting in a hexagram (aka the Star of David); and rotating-and-zooming (as shown above, [which is the final projection onto the material plane]). I see some of these elements in the crop circles and, short of taking sides, I'd like the virus construction viewpoint represented in crop circle analysis. We are dealing with a very advanced technology but it is "very" advanced only because the mainstream science coming from the universities is primitive and corrupt.
Twelve pointed
star
In practical terms the twelve
pointed construction is about the design of a clock's face. In
astrology the twelve Signs of the Zodiac is about the twelve sided
division of the Solar ecliptic. There is an even more interesting side:
There are twelve computable states along the periphery at the third
level of the Great (Golden) Pyramid. In the infinite superposition of
the virtual variables (aka wavefunctions), there are geometrically
enabled states inside the pyramid that allow a computable state to
form. Yes, infinities can be worked and the Quantum Pythagoreans
book gets into that and at all levels of the pyramid.
Eight pointed
star
Our construction for the twelve
fold division of a circle also divides a circle into eight exact
segments, or angles, because the 45 degree diagonals
are available for free from our twelve point construction if you
make full circles (and don't stop at the intersects with the central
circle). This is also true the other way: When constructing the eight
point division that is a regular octagon, the twelve fold division
happens as well if the central circle is drawn in full (and you don't
just mark the intersects with the cardinals). So here you have the
combined 8 & 12 point star construction. After a short Internet
search I did not find an 8 & 12 point star common construction {Apr
30, 2011}. I found one logical assembly having the Chinese
Zodiac on the outside circle and eight binary Paqua states on the
inside circle. (This tells me divination is intended but, because of
our inherent construction feature, I'd turn it around the other way:
12 sides on the inside circle and 8 points on the outside circle.
This is counter-intuitive but there could be [is] a form of Tai Chi
in this.)
Music of Venus
and other
planets
The common construction of the
eight and 12 pointed stars starts with the combined two and three
pointed stars. As you double the count the ratio stays the same:
3 to 2. (As you double the points you go up by an octave.) This is a
musical ratio and a harmonious one at that. What planets subscribe to
this ratio? It is not Venus-Earth but it is on the Venus
page.
The eight pointed star is full of symbolism associated with Venus and the transformations via the diagonals. The ccw octagon is harmonious and made by Earth-Mars interplay, too. So enjoy the eight-point star construction here via the cardinal and semi-cardinal directions but the Venus page has a lot more on the eight fold division of a circle, including the Hunab Ku symbol.
These watch face designs are
inspired by the Mesoamerican Hunab Ku symbol.
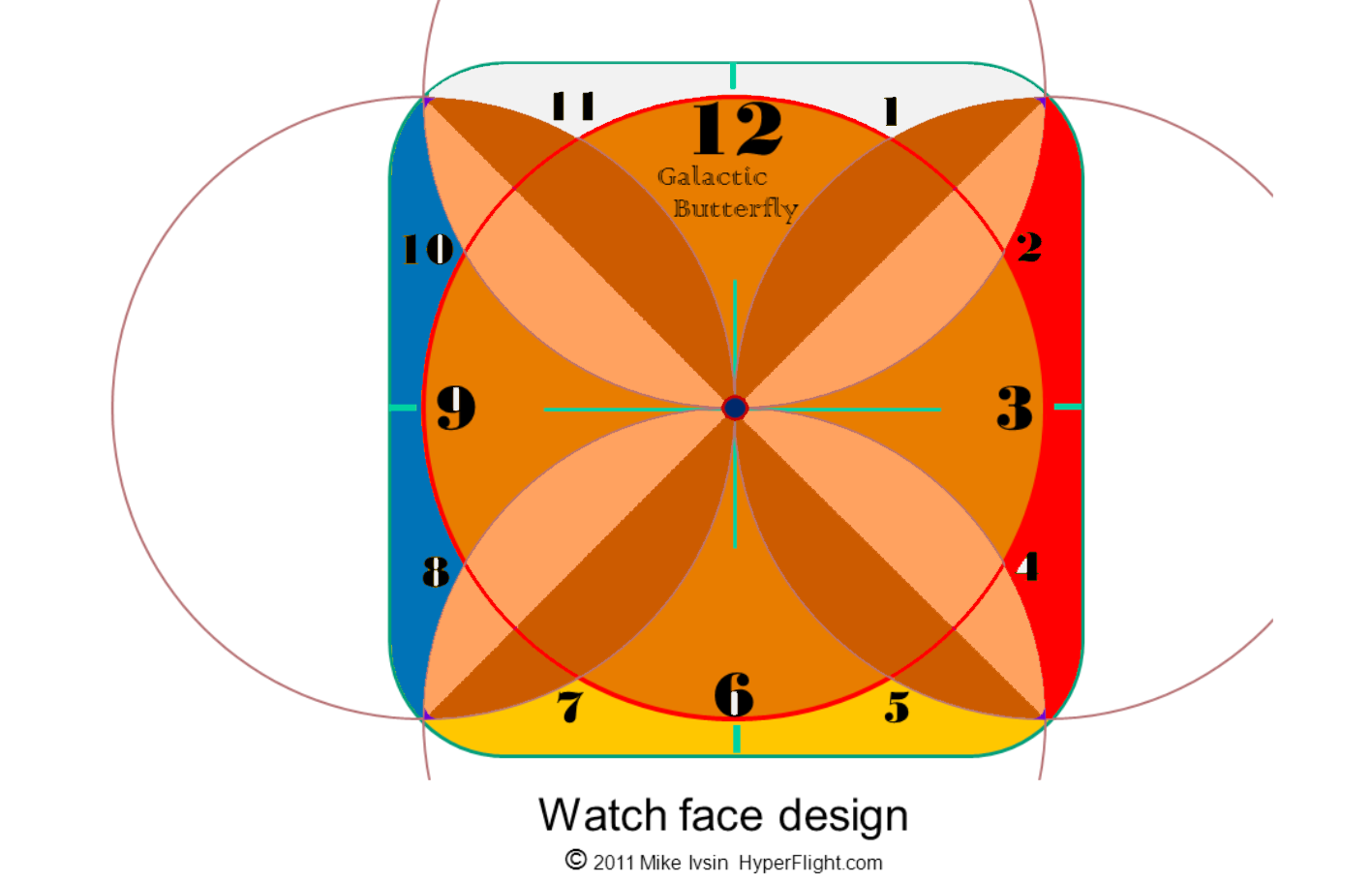
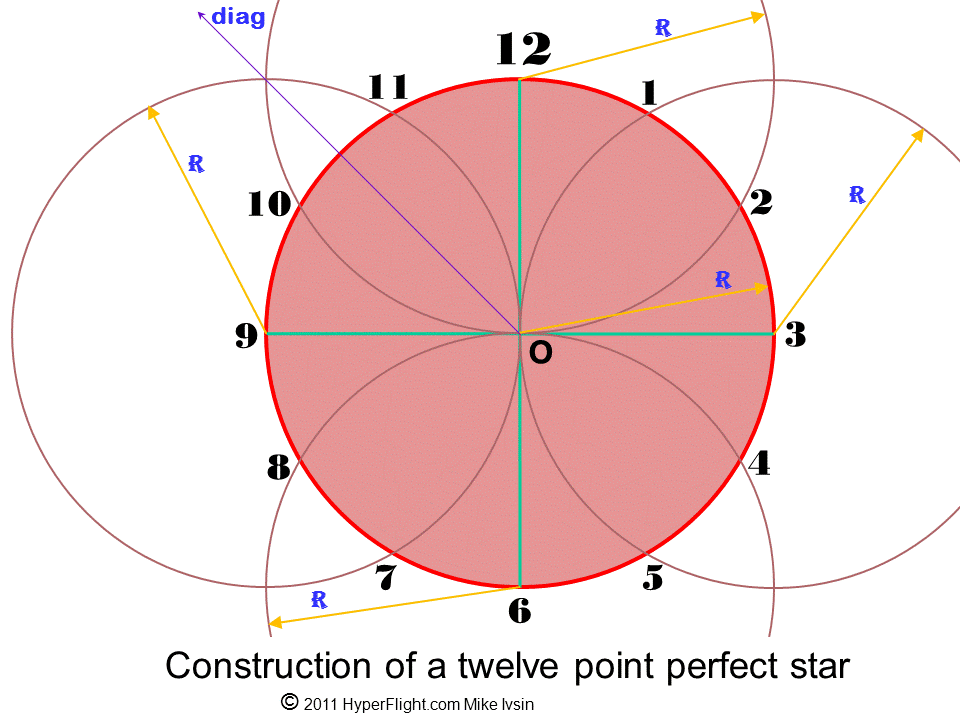 Instructions
for drawing
a 12-pointed/12-sided star:
Instructions
for drawing
a 12-pointed/12-sided star:
1. Draw a horizontal line and erect the vertical line. The intersect is the origin O
2. Draw a full circle of radius R around O. This will be the clock face
3. At each of the horizontal and vertical intercepts draw additional circles of the same radius R
4. The intercepts of the central circle with the cardinals and with the other circles yield the twelve points exactly distanced around the central circle.
Can you see how you could make a 24 point star using the diagonals? Almost every month we offer quick topics of general interest. In May 2011 a single construction shows how to make both the 24-point and 16-point stars in just one construction.

Perfect
star families
It
is easy to draw stars using geometry's tools, a straightedge and
compass. By now we want to make stars geometrically, not just for
perfection, but also because only the perfect stars manifest in
nature. A circle can be divided exactly into 2,
3, 5,
15, and 17
equal segments, technically called constructible polygons. (Some
exclude the 2-segment division because it yields but a virtual line
of a circle's diameter — but I include
it.) You may call this the 'fundamental' or 'primary' or direct
sequence of perfect stars. Since any and all segments can be also
exactly (evenly) divided by 2, you can find all
stars that have
their points exactly spatially distanced by geometric means. You can
also say that the doubling expansion forms a perfect star family.
For example, you can make an eight point star or a 64 point star from a two point star through simple halving of distances. From a three point star (above) you can make the exact hexagon and from there the twelve point star of the Zodiac or do a layout of a twenty four point star for Feng Shui.
Starting with a 2 point star — the only direct even star — you can construct 4, 8, 16, etc. stars you could also label the 'evenly even' sequence of stars. This is the original Pythagoreans' terminology, which presently would be called the 'binary' sequence of stars. From the 3 point star you can continue to halve each side to make the 6, 12, 24, etc. point stars. From the five-point star you can make the 10, 20, or 40 point stars.
Every perfect star with the even number of points will have symmetry about an axis and about a point. If you think there is no such thing as a two point star, it is on the Venus page and it is formed by the combined Neptune-Pluto 3:2 orbit.
The stars that are left out from direct and doubling constructions cannot be constructed exactly. For example, you cannot make a nine point star directly — or indirectly from a three point star. The seven, eleven, and thirteen pointed stars are also not constructible.
Numbers that divide a circle exactly could have a name of their own. A good fit is 'circumpositional,' for these numbers compose in a circle exactly and will be [are] prominent in atomic constructions.
Carl Gauss "recently" added the 17 sided polygon as the perfect star. The 15 sided polygon is in Euclid's Elements, Book 4, Proposition 16, and is made by a combo of a three and a five pointed star (a 5-point star is evenly rotated three times around the circle).
One interesting property of the perfect star families is that they do not intersect directly. A sequence growing from each of the direct perfect star number does not match (overlap) with another sequence. That is,
from 2 we get 4, 8, 16,
32, 64, 128, 256, 512, 1024, 2048,
4096, 8192, 16384, 32768, etc
from 3 we get 6, 12,
24, 48, 96, 192, 384, 768, 1536,
3072, 6144, 12288, 24576..
from 5 we get 10,
20, 40, 80, 160, 320, 640,
1280, 2560, 5120, 10240, 20480..
from 15 we get 30, 60,
120, 240, 480, 960, 1920, 3840,
7680, 15360, 30720..
from 17 we get 34, 68,
136, 272, 544, 1088, 2176, 4352, 8704, 17408, 34816..
Each member of the perfect all-star family has but one origin. Once a number becomes even it stays even. 3, 5, 15, and 17 make the only exact odd stars.
A circle is a zero pointed star having an infinite number of points. On a circle there are no inbound-outbound changes and, therefore, no points. Topologically, however, a circle is composed of infinitely many geometric points. This is a technical play on words. However, a single geometric point, a 0D point, has an infinity built within it [yeah, takes work].
Note that
360 does not divide a
circle exactly
260 does not divide a circle exactly (Mayan Tzoltek calendar). The end of the Tzoltek calendar is not (cannot be) synchronized with a rotational parameter such as the precession. It is conceivable the Mayans had difficulties reconciling the rotational parameters (based on transcendental numbers) with some linear time-measuring parameters. The numbers' unexact nature would lead to "disaster" conclusions. Well, yes, it could have been their own square-a-circle problem.
320 does divide a circle exactly and the 1/320 (reciprocal) is called ro by the ancient Egyptians
While a circle can be divided exactly by hours (24) or minutes (60), a circle cannot be divided by hours and minutes (24x60=1440).
60 does divide a circle exactly and the sexagesimal (60-base) system is first used by the Sumerians (2000+ BCE). Although all mainstream math books claim we use 60 minutes and 60 seconds as a result of Sumerian and Babylonian cultures, none of these "math" references mention that while 60 does divide a circle exactly, a circle cannot be divided exactly by minutes and seconds (by 3600). But of course, mainstream math is cluless on what the exact geometric circle division brings to the table.
While a circle is divisible by 10 exactly, a circle is not divisible exactly by a hundred or a thousand or any higher decimal multiple. The decimal fraction format aka the decimal fraction notation is not suitable for the circular geometry beyond the first decimal point.
Is it strange the Mayans — while having the positional notation of base 20 — had no sub-unity base-20 fractions? Perhaps not. Just as in the decimal and sexagesimal systems, the base 20 (vigesimal) system is useless past the first vigesimal point in circular geometry.
The perfect star families of numbers introduce some changes to our perception of universe building and how everyday reality happens to come about. Mathematicians can make all kinds of star constructions, in 2D and 3D – but only the perfect star families can begin to bridge the straight line energies, such as photonic energy, with circular orbits and orbital energies. Because the vast majority of the real energy in the universe is in the form of spinning or orbital energy – that is, energy having angular momentum, the perfect star families of numbers take the front seat. Scientists can draw all kinds of curves but these are usually fancies. Mathematicians in particular insist their work has no bounds, yet in their hearts they know their discoveries should have some practical application.
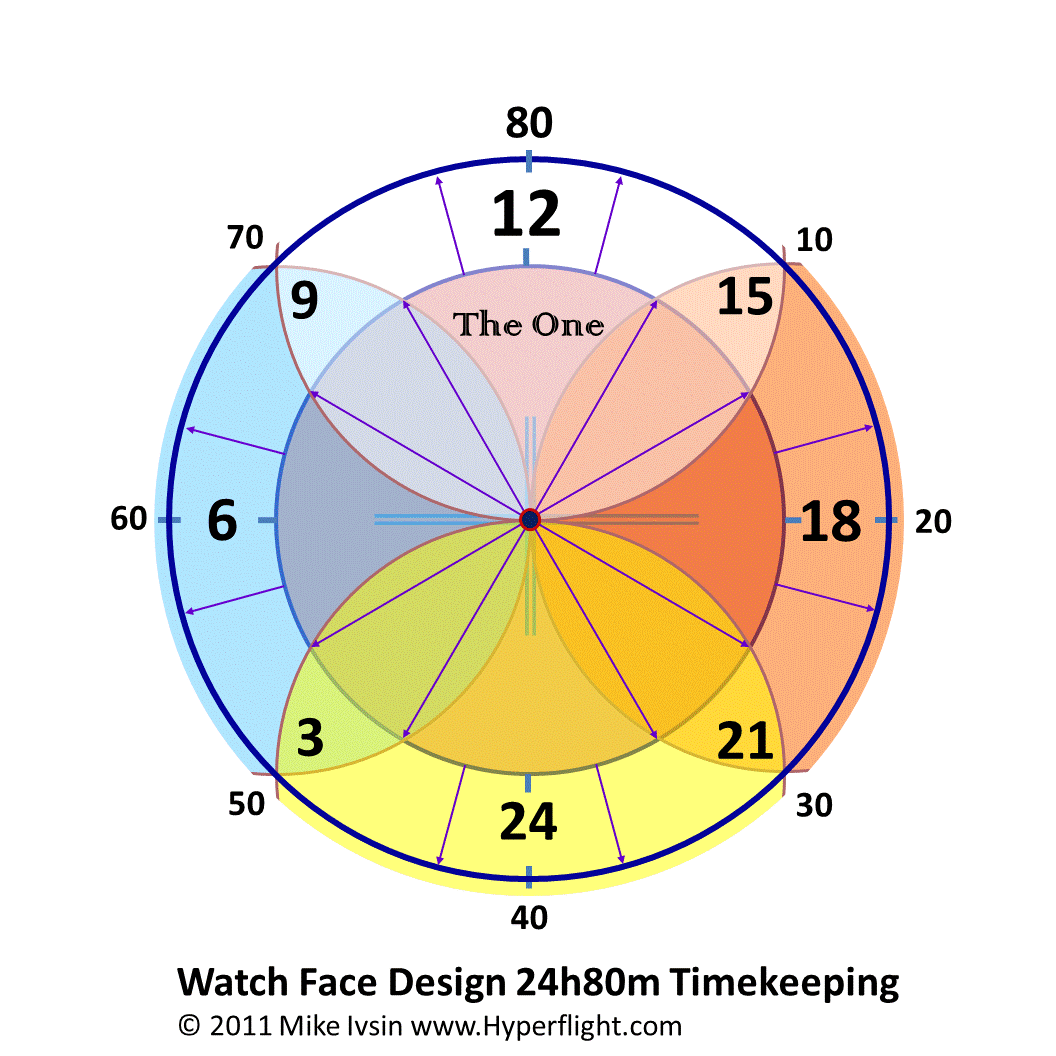
New
Timekeeping
Starting with 24
hours per day and having 80
minutes in an hour, every minute of every day (24x80=1920)
would divide a circle exactly. Such is not the case today. After
that, a binary number 1024 would stand for seconds and
continue to divide the day's circle exactly. One of the new seconds
would then be the exact 1,966,080th part of a day. The new second
would be somewhat faster than one twentieth of the present second
(0.05). While adequate for almost all sports without further
division, additional circle-exact divisions are always available –
something that is not possible to do today. (Once you lose the exact
circle division it cannot be recovered.) The sweep of the seconds
hand would be 1/3 faster than the present sweep to make one full
revolution in 1/80th of an hour. At all numerical markings in the
illustration on right –
the hours, minutes, and seconds –
would not be fractions. For example, the sweep of the seconds hand
spanning one half of the quadrant adds up to 128 seconds {May
11, 2011}.
One half quadrant, then, is 128 seconds or 10 minutes or 3 hours. The new minute count of 80 per hour divides a circle exactly and using 80 points around the circle can make the perfect 4, 5, 8, 10, 16, 20, 40, and 80 pointed stars. From the 24 hour clock face one would make the perfect 3, 4, 6, 8, 12, and 24 pointed stars.
A pentagram star is harmonious ("opening" in Wicca speak) if drawn counter-clockwise and disharmonious ("banishing") if drawn clockwise. Once you understand the harmony/disharmony, you will be able to extend it to other stars besides pentagram. Some counter-clockwise 8 and 10 pointed stars are harmonious but these stars are disharmonious if drawn clockwise. This does not mean the clock's hands rotation should reverse. See the Venus page.
Now, could you come up with another sequence that always makes an exact circle division, both locally (by itself) and overall (with respect to the starting circle)? Yes. Start with 20 hours per day and divide each hour by 192 minutes. Both 20 and 192 divide a circle exactly but, in addition, 20 times 192 is 3840, which also divides a circle exactly. Is there more to this than making new and different watches? You bet.
Tiling of pentagons and stars
Tiling
does not involve direct construction but only translation and/or
rotation in two dimensions. Translations are linear (straight)
motions. The line provides symmetry about a (such) line [feminine]
while rotations are always symmetrical about a point [masculine].
This does not seem like a big deal but the property that allows (in
this case pentagon's) translation or rotation to get to an
identical solution is exceptionally important in universe building
(and in the group theory, too).
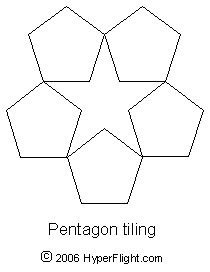
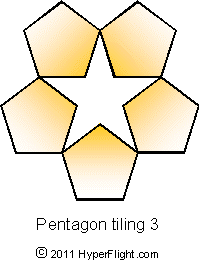

Tiling of five pentagons to make a cool five pointed star was (first?) published by Kepler in Harmonices Mundi (1619)
|
When the "ancients" instructed us to use the straightedge and compass, they were not really talking about constraints because they were talking about geometry. Rotation about a point is about the use of the compass. Straight movement (translation) is about a symmetry about a line and perhaps you could see now that the line of symmetry is a virtual line – that is, the line of symmetry is an empty slit. (Would you go as far as to have Justice brandishing her sword with a slit down the middle of the blade?) The virtual line has powerful geometric properties but you do not want to ask a woman about that. Not that you couldn't, it's just that the explanation is nonverbal. |
The pentagon template for the illustration on the left was obtained with MS PowerPoint by selecting AutoShapes .. Basic Shapes. Pick the pentagon object. On the newer versions it is Insert .. Shapes .. Basic Shapes.
If you tile five pentagons you get the five-point star in the center. Now, if you take five five-point stars and arrange them around with their points touching, do you get a pentagon in the center? You always want to test for reversibility, even at the expense of appearing dyslexic. Relations are reversible only under certain conditions and you want to know what they are. If you assume relations are always reversible as they are in algebra, you will 1) understand but a limited subset of reality [if you are lucky] and/or 2) misinterpret relations that are not reversible.
For example, if there is a quantum mechanical explanation of gas pressure, there could be a way of making the phenomena reversible. Now, how would you reverse the rotation of a light mill? (Give it a thought and get the answer.)
We readily apply force to get things moving. So, how would you reverse 'something' and have the force arise?
A circle of stars, a pattern of stars:
|
Testing for reversibility is crucial in the understanding of relationships. Dyslexia is a condition that is constantly reversing relationships in all modalities: verbal, tonal, geometric, written -- to see if the reversal possibly acquires another meaning, or if the reversal carries no meaning. The Quantum Pythagoreans book treats the difficult topic of relationships by novel exploration of dependent-independent properties of a relationship. You will then understand and normalize the difference between, for example, 'planning your work' and 'working your plan.' |

The tiling construction — that is, movement about a point and/or translation along a line, of some objects may result in the appearance of another object. This is at times referred to as "negative space." While it is true that the original object is real and in some respects positive, the 'negative space' label is but an introductory way of looking at it (and a left-brain way at that). A good way is to see this as the act of creation of the virtual object.
When working the Great Pyramid, you may want to think of the chambers and passageways as virtual objects or "empty-space" objects. It really helps.
|
Self test:-) Straighten up two adjacent fingers. Do you see a difference if you think of these fingers as two closely spaced pencils – or as an empty slit or space that is between the pencils? Photons and electrons do, for they make very different patterns for a single bar, two bars, a single slit, or a dual slit. For brainwork: 1) How is it possible, and 2) What is the utility of the result that one pattern ends up in the left side of the brain while the other in the right side? |
|
Geometry versus arithmetic
|
|
It is now time to visit the angles of a circle. Can we map the angles in such a way as to obtain correspondence between geometry and arithmetic? What's your angle? |
|
Arithmetic
makes it strange What then is the advantage in dividing the circle exactly by this or that number? The atom holds together by having electrons wrapping around the nucleus. Because the electron's momentum is also a wave (de Broglie), the electron's wave must evenly, that is exactly, close upon itself to form a standing and a round wave that is symmetrical about a point. To the Pythagoreans the numbers are everything and this is because numbers actually create things. The mainstream scientists' argument that "computer's representation of an irrational number is close enough" is, unfortunately, not relevant to atomic construction. Scientists just do not know how to interpret 'precise' and 'exact' in an applications setting. The scientist can divide the circle by nine to a very large number of decimal places, but there will never be a wavelength that would fit nine times around the circle of the orbital. Incidentally, 'fit' is the original (superior?) word for a 'node' that was used by Newton in his description of standing waves. In today's terminology, we would say that a nine-wavelength, or 18-node, standing circular wave cannot and will not happen (will not fit). Numbers 7, 9, 11, 13, 19, 21, 22, 23, 25 and others cannot divide a circle exactly. Most of these numbers are incomposite (prime) numbers. Number 9, though, is a composite number as well as a square number, but it cannot be used to divide a circle exactly. [Does this mean the Chinese Emperors could not sing? Having said that, they might have been good golf players.] Number 5 is incomposite but can be used to divide a circle exactly. What is needed, then, is a class of numbers that compose in a circle, instead of just being composite numbers (composed of products of other numbers). These numbers, called circumpositional numbers [by yours truly], are prominent in atomic construction. Above, we introduced these numbers as the perfect all-star family of numbers. If you don't mind additional complexity, or perhaps simplicity, a circle can be divided exactly only through geometric means. Another way of saying 'geometric means' is 'spatial distance means.' Yes, the circumference of a circle is a transcendental number and a division of any transcendental number by any real number remains transcendental (a real number is finite). The computer can use only real numbers and the length of the circumference is then rounded off if it is to be stored in a computer. What this also means is that a computer cannot give you a perfect star. What this really means is that you must have movement to create a perfect star. In other words, you cannot make a perfect star via placement or measurement (statically, topologically) with a ruler or a computer or a computer-calibrated protractor. As a Pythagorean you might realize that you cannot construct a perfect star without a compass – that is, you need rotation to complete exact constructions. A compass is the only tool that allows you to enter 2D from 1D. In other words, a compass allows you to turn. A larger implication is that there must be movement even at the atomic core level — and under radial symmetry the movement is also about frequency. (You might guess here is one of the gateways to gravitation and yes, the philosopher's stone opens up to the alchemist.) The necessity of movement permeates everything. Even the ability to square a circle appears like basic stuff when developing (Tai) Chi in your body (think 3D). |
|
Arithmetic
makes it practical Now that all people are smart enough to handle as "huge" number as 2040, is it time to make our circle geometry as sophisticated as it can be? Are you ready for the sum of internal angles in a triangle to equal 1020 degrees instead of 180? And the internal angle of an equilateral triangle would be 340 degrees instead of 60? Even if you could legislate the change – and during the French Revolution they "legislated" 100 degrees in a circle and 100 minutes in an hour -- the bottom line is that there is no perfect number for a quantity of degrees in a circle that would be a whole number or even a rational number. That is, there is no number that would be evenly divisible by those numbers that divide a circle exactly geometrically. In the example of the 2040, this number is not evenly divisible by 16. [Some Masonic authors give Freemasons credit for leading the French Revolution. If so, they would certainly be quite ignorant on what to do in the aftermath – all their Gs notwithstanding.] Whole numbers and rational numbers are called real numbers – a good name. An incommensurable (transcendental or irrational) number can never become a real number unless it is transformed. The transformation is irreversible because we cannot save an irrational number such as SQRT(2) in a computer and retrieve it as (convert it back into) the original irrational number without first taking a nip off the number – think Ouroboros and visit Circle and Pi. Reversing the transformation calls for addition of the virtual energy [think Isis and possibly Thoth if you are familiar with his eye restoration story]. If you want to get deeper into transformations of rational (real) and irrational numbers – think ancient Egyptian fractions [here, you will need to appreciate three things: 1) Ancient Egyptian fractions are quite sophisticated; 2) Present day scientists are clueless as to the ancient Egyptian fraction applications or origin; and 3) Our present civilization is not necessarily advancing.] When dividing a circle with the straightedge and compass, the goal is to make the number to become, for the number's geometric construction creates something specific to that number. There is, then, more to numbers than philosophy, and you may want to visit the original number apps guys, Pythagoras and his fellow Pythagoreans. There is a treatment there of real, virtual, and irrational numbers. Irrationals and transcendentals are in the family of incommensurables but transcendentals are not constructible through the Pythagorean Theorem (from 2D of the curve to 1D of the hypotenuse), while additional differences between irrationals is based on applications. [There are good and bad numbers and some of them have an infinite mantissa.] |
|
What does a star in a circle represent? What is the meaning and symbolism of a star inside a single circle? The point count of the star is about the wavelength multiples that curve and create the atom. Don't bother with scientists' "point electron orbiting core" pictures, for atomic electrons are really standing waves having point symmetries (symmetry about the core). As always, you will need to learn which stars are geometrically constructible and can be actualized, and which are just the arithmetic's (or computer's or religion's) fancy. Is the atomic core composed of standing waves? You bet. Scientists have way too much invested in the solid and static core hypothesis and so it is safe to talk about the pulsing and standing waves of the core. Scientists are way off and, for example, they made up "strong nuclear force" because they do not understand the wave nature of the core. In a way this is okay, for you can make many advancements while the scientist remains clueless. For example, the core's shape is not necessarily spherical. With all their equations, scientists think highly of whatever it is they describe with them. Saying that the scientist will remain clueless is no idle talk, however. On our Circle & Pi page we also highlight the inadequacy of algebra, for algebra's constructs cannot deal with the operation of equivalence. Algebra completely misses irreversibility, too. As a Pythagorean you want to figure out what entity will prevail in the interaction with a standing-wave electron and with a standing-wave proton. Why, could you then do a precision surgery on the atom? |
Seven
pointed star
A circle
cannot be divided by seven exactly. Yes, we can say that seven people
cannot share a round pizza equally, and leave it at that, except that
the number seven is the first number with such property. When things
are happening inside a circle —
that is, when things are spinning and evolving, the wave folding
encounters the number seven and consequent inability to fit around
the circle (and make a perfect star). When you examine the
Mesoamerican Hunab
Ku symbol, there are two seven-sided areas (heptagons) and now
the challenge is to explain that. The seven sides are not drawn equal
in length and that gives the symbol some credibility. The heptagons
pivot into 3D and now it gets really intriguing. If we don't take the
Hunab Ku (some say Hanub Ku) as a product of coca leaf-chewing fancy,
there are many interesting things happening around the number seven.
I'd be careful in using the seven pointed star. Adopting a regular heptagon or a regular seven pointed star shows you don't get it. So I'd draw the star free hand or use an irregular heptagon. Mayans have a gap in their seven-segment Ouroboros too.
 The
Goddess Seshat's symbol from ancient Egypt is a contextualized
seven-leafed plant (she is a scribe, which means she is a magician).
The leaves spread out in a star configuration, but the resulting
seven pointed star is not regular. [If you think the symbol is a
cannabis plant then that's fine by me. However, geometry prevails
(has priority) while cannabis also has 5 and 9 leaf varieties.]
The
Goddess Seshat's symbol from ancient Egypt is a contextualized
seven-leafed plant (she is a scribe, which means she is a magician).
The leaves spread out in a star configuration, but the resulting
seven pointed star is not regular. [If you think the symbol is a
cannabis plant then that's fine by me. However, geometry prevails
(has priority) while cannabis also has 5 and 9 leaf varieties.]
The Statue of
Liberty has a hair dress with seven rays. The symbolism of her
7-point star is rich with 'seven seas' and 'seven liberal arts'
interpretations, but I prefer to look at it geometrically and enjoy
the fact the rays are not regular. 
|
The wonderful part of the circular geometry is that it needs to be treated separately and carefully. Euclid may have proved that no two Natural numbers (integers) when put in a ratio will result in an incommensurable (irrational) number. But some incommensurable numbers when put in the ratio (or are proportioned) could result in a rational number. You may want to reflect on what it means. As far as Euclid goes, not much. After all, Euclid talks about what does not happen. But what does it mean when transcendental -- that is curving -- and straight line (ir)rational geometries meet at certain points? Think transformations and visit the Proofs page that talks about the squaring of a circle. Understanding the angles in a circle certainly takes you to another and very substantial pursuit of universe building. Looking back, is there some work that was done just in this area? But of course, you'll have to step over the reductionists, yawn at the popularizers, and laugh at people who allow to be called experts. [I'd bet 10:1 they will talk about running out of energy.] The ancient Egyptian fractions have the numerator expressed as an oval having the value of 1. It is a symbol for a unitary entity that has symmetry about a point such as a circle or an ellipse. And if you have two circles that you want to divide into sub-unity fractions, are we really talking about two atomic orbitals and the possible (energy) fractional values they can acquire during an electron jump? So now you have yet another quest to make. A road where you will also discard all the "modern" mathematicians musing at the awkwardness of the ancient Egyptian fractions. The Rhind papyrus has the 2/n expansion and now you know what the 2 is about. Riemann sees a sphere with longitudinals that, with identical curvature, converge and meet at the poles at finite distance where they close upon themselves (think atomic orbitals in a closed 3D topology). Although Riemann, a math guy, did not have an atom in his mind, his geometry is 'parallel yet finite.' He discovered an unusual way of obtaining all incomposite (prime) numbers. We have three book reviews on this remarkable individual. Then there are the scales of the fish [yeah, the dumb fish]. The sweeps of the scales subtend a particular angle. Do you think a fish could fly or extract energy from the swirling water around it by using the geometry of its scales? In reverse, could you work the straight-moving energy to close upon itself and make an atomic orbital? Think pyramid geometry and Schauberger. |
|
Illuminati,
Masons and New Order Guys. Pythagoreans, too So you want to ask if the result you reached is beneficial or not. If you think accusing someone of evil thoughts is beneficial to your religion then you are a part of a religion that is sustained by attempted oppression of others. In short, your religion is not based on truth. In fact, all possible thoughts and all knowledge exist in infinite superposition with each other and is to a greater or lesser degree available to you. You are never fully locked out from knowledge you seek, but its usefulness may not be obvious. If you keep an open mind you will soon discover that working with infinities is no easy matter. Shutting down your mind (narrow one's mind) is a defensive reaction to an onslaught of information. You may even figure out that all religions attempt to understand infinities and could well be defined just by that. So relax. Infinities can be worked but they need different methods. Things that don't add up simply won't happen. [So what is my Pythagorean take on the 7-point irregular star? It is about the creation or release (liberation) of energy. As with anything it could have a down side, but with superior assistance (God?) it can be managed and be useful. Oh, the thing about God is that you have to ask. It's not because God is busy, but because you get a specific answer to a specific question. Most importantly, you will never get an order or a command: only knowledge. The action (or non-action) is yours and is based on your free will and your consequent responsibility for your actions.] |
Historical
Note
Johann Balmer
was the guy who opened wide the barn doors of quantum
mechanics. Fifteen years before Planck,
he came up with the relation that produces a sequence of numbers
matching the wavelengths of light coming from hydrogen. These are not
just any numbers –
they are wavelengths corresponding to particular electron jumps and
no other. Balmer did for quantum mechanics what Kepler
did for gravitation: He came up with the math equation that matched
known experimental data and made successful predictions of other new,
yet undiscovered, wavelengths. But there is a bit more to it. Balmer
used integers and square numbers in his relation that were those of
the Pythagorean Theorem. Well, good ol' Pythagoras was not only right
all along but the breadth of his –
some say HIS –
teaching was also the foundation of quantum mechanics. Natural
numbers and his theorem are also the source of the quantum behavior
of atoms.
|
|
This topic is expanded and has a page of its own. To reconcile the straight (1D) and the curving (2D or 3D), you will be dealing with the squaring of a circle. Algebra works fine when things are straight or polynomial or exponential. Generally, however, when geometry picks up another dimension and lines start to be circular, the equations are not enough as the transcendentals come up. The relationship of the squaring of a circle to this page's perfect division of a circle is in the possibility of linearizing the curved segments (arcs) of a circle and then making a tractable exchange between curving and straight topologies. So there is a continuation to 'how to draw a star' and it deals with energy. Can we say that geometry is about energy? Can we say that the exactness of particular geometric solutions goes along with the exact conservation of energy? Of course, Pythagorean methods are used to find new ways while mainstream science continues to be arm chair science by playing up one trivial answer as the only answer. At times politicians pick up the 'square a circle' analogy and then you should know they are trying to find excuses and "explain" failures to their supposedly dumb constituents. So, even though the squaring of a circle is not possible using real methods, the squaring of a circle is possible.
Alchemy
The
complexity of our environment is oftentimes worked through alchemy.
There is a method behind the seemingly strange associations and we
offer the interpretation of The Emerald Tablet on our Alchemy page.
Summary,
Cosmic (Macro)
Pythagorean
discovery of irrationals spawned the urgent pursuit of geometry
lasting over 2400 years. Kepler brought arithmetic to the forefront
by establishing the mathematical and arithmetic relations of heavenly
orbits. In effect and in fact, Kepler introduced the parameter of
time in the mathematical context, which made it possible to make
planetary position forecasts —
forecasting being Kepler's life long passion. Because any two
gravitationally interacting bodies always have a solution, the
parameter of time derived from such periodic solutions is also
repeatable (periodic) and time can be used to make forecasts. Even
though time is always a derived (dependent) variable, the
mathematical solution establishes reversibility and allows the time
parameter derived from this
system to be used.
(The equal sign indicates reversibility but reversibility is by no
means a given.) Another way of seeing the mathematical solution and
consequent time reversibility is that the spatial distance (space)
and time form an overlay. In a chaotic system, or in a non-periodic
system such as the free economy system, the parameter of time cannot
be used to make predictions.
Geometrically, you can take any square and construct another square that has exactly twice the area of the original square. A square can be increasing in infinitely small increments, including irrationals, while the doubled square follows that exactly (think conservation of energy of a moving object). This is something your computer cannot do. If you think this is no big deal and it is something for the ancients to contemplate – that's fine. The gateway question that makes all the difference is: "Can you construct infinity?" Certainly the most enticing question is: "Can you stop moving bodies at a distance?"
Summary,
Atomic
(Micro)
Light
is understood as moving or standing linear -- that is,
straight, waves following Newton's analysis of fringes (first
observed as fringe rings). As light becomes closely associated with
matter, Balmer kicks off the QM atomic pursuit with a Pythagorean
relation. A wavefunction is understood as a probability distribution
of an atomic particle — a great step
forward by Heisenberg and von Neumann. A moving particle has
momentum but momentum can also be worked as a wave —
a second great step, this time by de Broglie. A moving electron now
gets to become a wave as well, but this wave must curve –
that is, become circular, and close upon itself in a symmetry
about a point (about a core). The circular (or rounded) electron
orbital and the straight path of light need to be energy-reconciled
through the squaring of a circle — the
first difficult hurdle.
Ether is taken out of science's purview, which is the Great Reduction making the scientist that much poorer in the end. Scientists cannot make headway and talk about impossibilities. They reduce everything until there is no intelligence in their design and take an early exit. (In their last hurrah the angry mob bashes and trashes cold fusion.) Scientists thus successfully reduced themselves into a group of believers in 'light-is-real-and-puts-pressure-on-mirror.' While much of today's physics rests on it, the scientist has no guts and no brains to perform the actual experiment measuring the presumed pressure light puts on a mirror. Scientists are not able to face up to the truth that a light beam does not and cannot put pressure on a mirror and so they are stuck perpetuating, defending, and proselytizing their dogma.
Meanwhile, geometry is receiving new impetus by reviving its superiority over arithmetic and algebra. The golden proportion, the infinite and instant wavefunction superposition, the understanding of irrational and transcendental numbers, linearizing particular segments of a circle, and the possibility of creating electron waves with harmonics-series energy components just might get the atomic understanding going again – perhaps in another country, perhaps by another group of professionals.
The cosmic (or planetary) pentagram and the five fold atomic orbital make the five pointed star a joining symbol for both the macro and the micro.
While the atom's orbitals are symmetrical about a point (have radial symmetry), the valence orbitals in a molecule need to close around two points of symmetry (the cores of the atoms are some distance apart). Yes, the Hyperstar has an answer to that on our golden proportions page. {Dec, 18, 2009}
Pentagon Pyramid
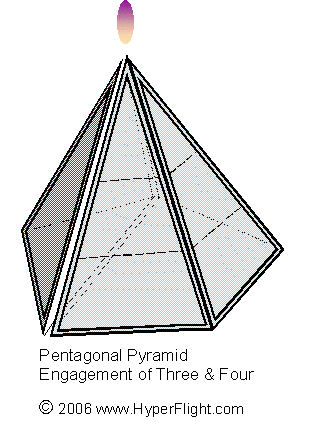
|
Self-test:-) If you are not happy about the pentagon base and/or the pyramid being "split up" or "broken up" or "separated," you are not getting the picture. You may want to think about the red part as being the tangible component while the blue part is the intangible (knowledge, virtual) component. If that does not help, stay in 2D [earthbound?] where the pentagon is continuous. If you think Two rather than Four is feminine, you are very close. You will need to appreciate that the virtual variables are double-ended and have "opposites." Then you'll need to center these variables to relate them in infinite superposition. (Quantum Pythagoreans book helps in this area too.) The engagement of Three and Four is just that: It can be supportive in some contexts and in others it could be conflicting, in which case rebalancing work is needed. |
|
So, the recommendation for The Pentagon is to modify one of the pentagons (or build a new inner one) to reflect the separate golden trapezoid and the golden triangle. The new construction slants upward toward a point. It does not need to top off in a point as long as the edges are converging toward a point. (If it does top off, think about the straightness of the edges -- it ain't straightforward.) |
|
|
|
There
is one symbol that uses a circle framed by two vertical lines. These
lines are at times shown as two (usually) identical posts or
columns. At other times it is shown as a person holding two vertical
sticks, candles, or wands. This symbolism, however, is not about the
3 vs. 4. Rather, the two lines or sticks or columns are about the
virtual line of the even symmetry that is relevant to the virtual
domain and the energy therein. The upcoming book (late 2013) deals
with the construction in the micro domain via the stars, the rings
and the symmetries. Yes, knowledge is organized energy. |
Three and Four must remain separate even though they are also joined. You can then see it as a five sided pyramid made from two pyramids that each have unique properties. The overall 3D structure has almost all numbers in it but the point is that the numbers must play together to their best advantage (rather than just being represented).
Do you see the number zero? Or is it the infinity? Could it be both? Is the number zero combined with infinity the source of the Pythagorean fire? The root of the pyra-mid? The Central fire? The hearth of Zeus? Archimedes' fulcrum of the heaven and the earth? Just a plain (free) electron? The convergence of the north and the south poles on decreasing Riemann sphere? A point of the zero dimensional (0D) geometric construct? 'The One' of alchemy? Something even smaller than the infinitesimal of Newton and Leibniz? The dot in the semicircle on the AUM symbol? A computational construct for all of the above from "all of the above?" The top dot of Tetractys? My favorite: The eye Thoth sends to look for Tefnut when she runs away to Nubia (yes, the eye finds her).
If you think this pyramid is about marriage, you are on the right track. The Three [male] and Four [female] are joined through the point of the infinite. This joining is applicable to the actual marriage where the joining is through God – all there is. The alchemical marriage would have the female part becoming more abstract although the four-sided pyramid geometry continues to be needed for dealing with the infinite. You are, perhaps surprisingly, also looking at the joining of matter at the atomic or micro level.
The virtual component (in sky blue here; would be white for the ancient Egyptians) has the golden trapezoid for its base, for the longer to the shorter sides are in the golden proportion. The real component has one of the golden triangles for its base.
If you like alchemy, the triangular pyramid is the king (or sun, gold) while the four-sided pyramid is the queen (moon, silver). Yes, this is the 3 vs. 4.
In the ancient Egyptian context, the crown of Egypt has two separate components: The white (upper, virtual) and the red (lower, real). The gap between the two is the ancient Egyptian blue crown and is invoked at war. (The gap is white in our pentagonal pyramid.)
|
|
Pythagoreans use the knowledge of numbers to arrive at harmonious and stable systems. Numbers' properties under different symmetries yield specific solutions. Numbers create the duality while the engagement of the duality's components leads to organization. Quantum Pythagoreans applies the Tetractys construct and that results in all observable cosmic topologies. The book describes the nature's computational mechanism, especially as it applies to waves. What it takes to transform energies. Your body is a component and it is not the only one. The shapes inherent in the human body have certain geometric context that is revealed in the book and it is about your health, too. You will like and appreciate the simplicity and the power of numbers. The Pythagorean management of numbers takes you on the road to reality and invites you to drive it as well. |
Go![]() or select another topic from the gold post
or select another topic from the gold post ![]()
HyperFlight home Portal
in new window
© 2005 -- 2013 Backbone Consultants Inc. Copyrights Information
Last update August 12, 2013



 2)
Two concentric circles around the star make it the cosmic or planetary
pentacle and the two circles are the orbits of Venus and Earth
(can be computed via modulo math from the clockwise 8:5 orbit ratio
and in the illustration on left the orbits are to scale). Points are
between and close to the midpoint of the two orbits and the pentagram
rotates (why that is so is on the
2)
Two concentric circles around the star make it the cosmic or planetary
pentacle and the two circles are the orbits of Venus and Earth
(can be computed via modulo math from the clockwise 8:5 orbit ratio
and in the illustration on left the orbits are to scale). Points are
between and close to the midpoint of the two orbits and the pentagram
rotates (why that is so is on the  3)
Separated but interlocked circles (rings) with centers at the
"hips" of the pentagram show two separate atoms joined in a
molecule, which I call the hyperstar pentacle. This is new and
I don't presently know of anybody applying the hyperstar pentacle.
Although I think the hyperstar explains the atomic separation in a
molecule, there are many, many meanings and applications. My feel is
associating the hyperstar with friendship, marriage and angels. I
like using it in Tai Chi and here is
3)
Separated but interlocked circles (rings) with centers at the
"hips" of the pentagram show two separate atoms joined in a
molecule, which I call the hyperstar pentacle. This is new and
I don't presently know of anybody applying the hyperstar pentacle.
Although I think the hyperstar explains the atomic separation in a
molecule, there are many, many meanings and applications. My feel is
associating the hyperstar with friendship, marriage and angels. I
like using it in Tai Chi and here is  Pythagorean
pentagram/pentacle symbolism is a bit
different and possibly more sophisticated if you think in the
square-a-circle context. The pentagram is encircled once and then a
second ring is added as a piece of jewelry. The second ring is then
at the right angle to the first. (The illustration is from Secret Teaching
by Manly Hall.)
Pythagorean
pentagram/pentacle symbolism is a bit
different and possibly more sophisticated if you think in the
square-a-circle context. The pentagram is encircled once and then a
second ring is added as a piece of jewelry. The second ring is then
at the right angle to the first. (The illustration is from Secret Teaching
by Manly Hall.)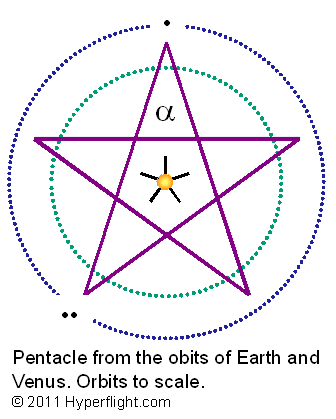
 (Under odd symmetry every point has a second point on the other side
of the center of rotation.) If you want to unambiguously show the
star's point-up or point-down placement on a coin, you have to place
the star next to a non-symmetrical reference such as an animal (or
introduce the even/mirror symmetry, which is the case in nature). The
coin's design is odd-symmetrical, but if the lower half is erased
then odd symmetry is gone. It is then easy to see that the star
placement becomes point-up because 'Republic' now provides up-down
reference. So you can appreciate that "up side down" is not
a given under odd symmetry alone because when your reference is but a
point (such as the Sun in the center), you could see the star one way
looking from the center and the opposite way looking into
the center.
(Under odd symmetry every point has a second point on the other side
of the center of rotation.) If you want to unambiguously show the
star's point-up or point-down placement on a coin, you have to place
the star next to a non-symmetrical reference such as an animal (or
introduce the even/mirror symmetry, which is the case in nature). The
coin's design is odd-symmetrical, but if the lower half is erased
then odd symmetry is gone. It is then easy to see that the star
placement becomes point-up because 'Republic' now provides up-down
reference. So you can appreciate that "up side down" is not
a given under odd symmetry alone because when your reference is but a
point (such as the Sun in the center), you could see the star one way
looking from the center and the opposite way looking into
the center.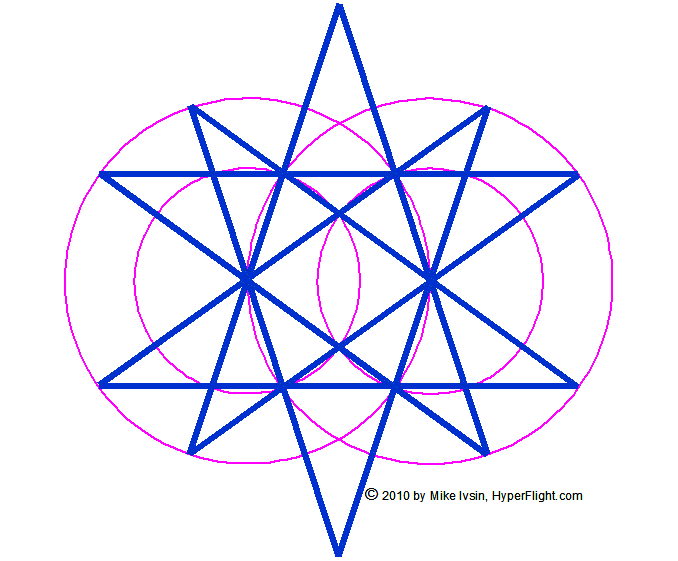 Overlaying
two opposing hyperstar pentacles
Overlaying
two opposing hyperstar pentacles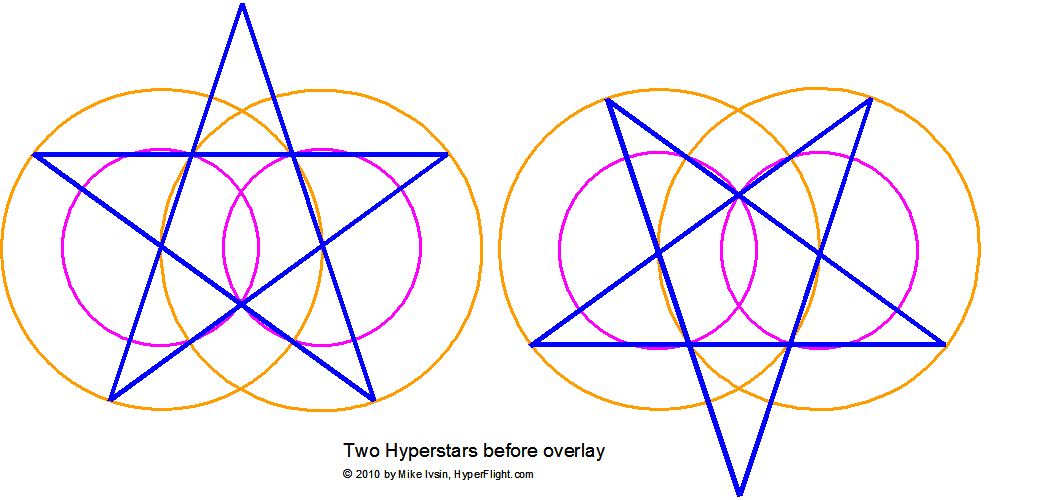 ,
the up-and-down points from the two pentacles
make a ten-pointed hyperstar, which is not a decagon nor a hexagon,
either regular or not -- yep,
,
the up-and-down points from the two pentacles
make a ten-pointed hyperstar, which is not a decagon nor a hexagon,
either regular or not -- yep, 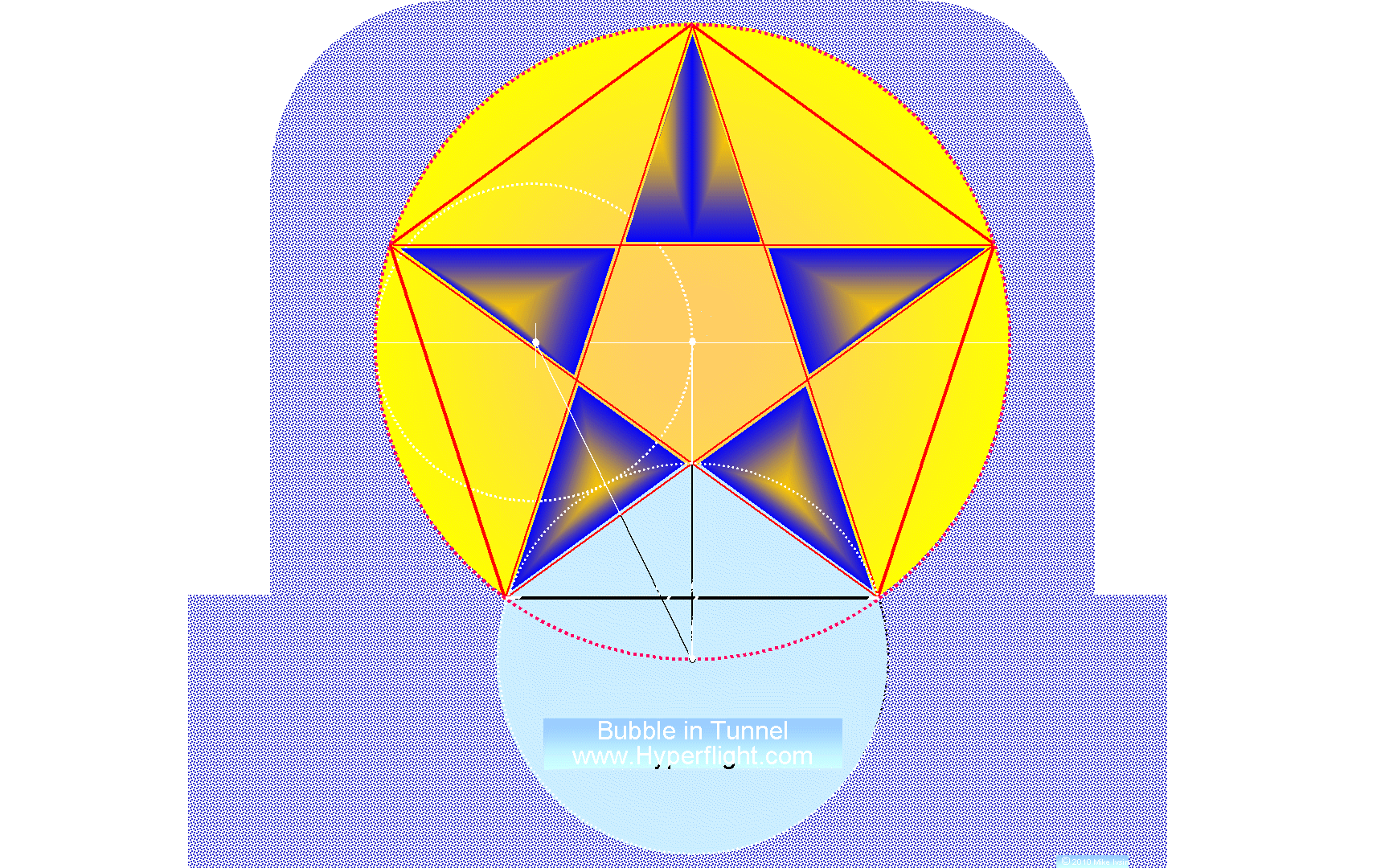








 Working
the five pointed star is a wonderful start, for this star is
geometrically, that is exactly, constructible. Constructing the real
universe is, moreover, the greatest show there is. Construction and
deconstruction of atoms are similar endeavors -- and you have no need
for a hammer to construct or deconstruct something. The forces
therein can add up in controlled fashion, too. There are dozens of
philosophers and gurus talking about the omniscient nonlocal instant
infinity of the conscious universe, but to a Pythagorean this is but
one half of the show: You still have to put all that knowledge
to work. Yes, we have pictures. The upside down star has no negative
meaning in the micro domain. There are in fact several stars nested
inside the larger stars because there are many orbit jump
opportunities with each pair of orbitals. Yes again, ALL triangles
are golden.
Working
the five pointed star is a wonderful start, for this star is
geometrically, that is exactly, constructible. Constructing the real
universe is, moreover, the greatest show there is. Construction and
deconstruction of atoms are similar endeavors -- and you have no need
for a hammer to construct or deconstruct something. The forces
therein can add up in controlled fashion, too. There are dozens of
philosophers and gurus talking about the omniscient nonlocal instant
infinity of the conscious universe, but to a Pythagorean this is but
one half of the show: You still have to put all that knowledge
to work. Yes, we have pictures. The upside down star has no negative
meaning in the micro domain. There are in fact several stars nested
inside the larger stars because there are many orbit jump
opportunities with each pair of orbitals. Yes again, ALL triangles
are golden.
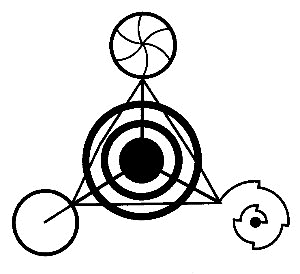 On
July 17, 1991 at Barbury Castle there appeared a crop circle named
the Tetrahedron (a triangular pyramid). For its 20th anniversary we
have a
On
July 17, 1991 at Barbury Castle there appeared a crop circle named
the Tetrahedron (a triangular pyramid). For its 20th anniversary we
have a  Here
is a poster for a Graphics show I had in Prague (where I teach now)
in February 2013.
Here
is a poster for a Graphics show I had in Prague (where I teach now)
in February 2013.

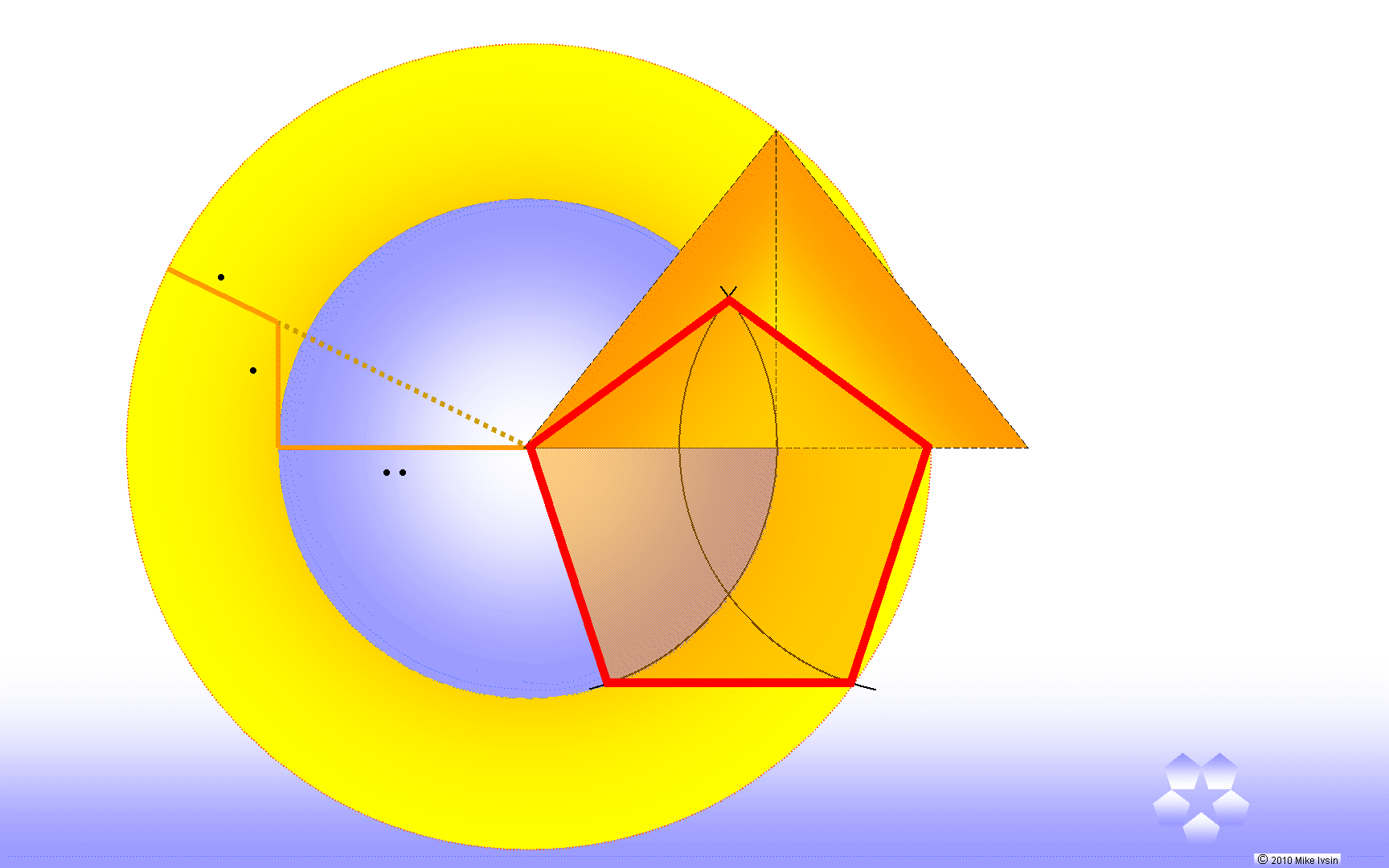
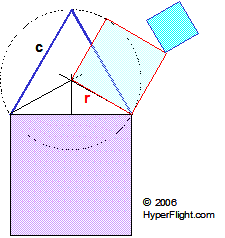 You
can be fairly certain that the person will try to partition the
square in some way but the solution is to erect
a triangle on the square's side and then obtain the radius for the
circle that covers the triangle. Radius r
is the side of the new square. [In our case the bad souffle does not
cave in but runs over the rim.]
You
can be fairly certain that the person will try to partition the
square in some way but the solution is to erect
a triangle on the square's side and then obtain the radius for the
circle that covers the triangle. Radius r
is the side of the new square. [In our case the bad souffle does not
cave in but runs over the rim.] This
pentagonal pyramid is on Mars. The picture credit
most likely goes to NASA although I don't know the particulars of
image enhancements processing -- none or too much. Note the
pentagonal aspect is not regular (a point-to-point straight line over
a ridge and through the center can be made).
This
pentagonal pyramid is on Mars. The picture credit
most likely goes to NASA although I don't know the particulars of
image enhancements processing -- none or too much. Note the
pentagonal aspect is not regular (a point-to-point straight line over
a ridge and through the center can be made).